Предмет: Геометрия,
автор: Fl1er
Круг радиуса R обложен четырьмя равными кругами, касающимися данного так, что каждые два соседних из этих четырех кругов касаются друг друга. Вычислить площадь одного из этих кругов.
Ответы
Автор ответа:
0
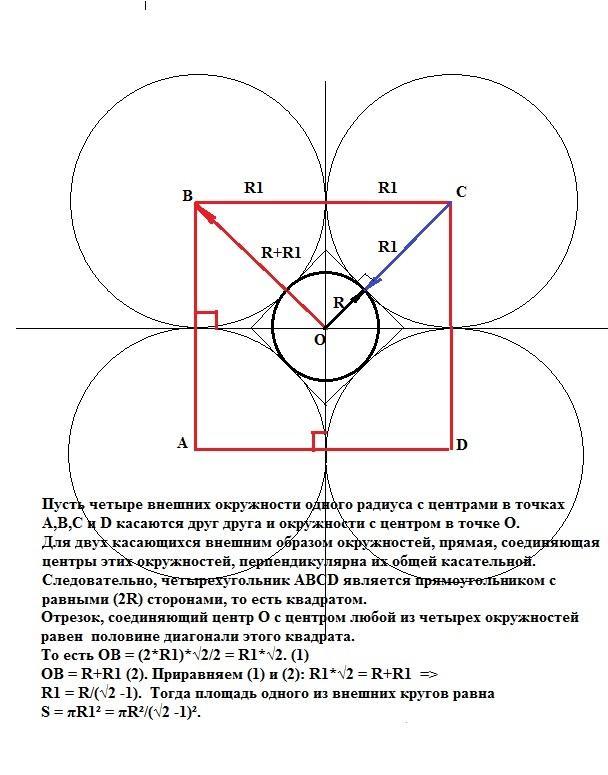
Пусть четыре внешних окружности одного радиуса с центрами в точках А,В,С и D касаются друг друга и окружности с центром в точке О.
Для двух касающихся внешним образом окружностей, прямая, соединяющая центры этих окружностей, перпендикулярна их общей касательной. Следовательно, четырехугольник АВСD является прямоугольником с равными (2R1) сторонами, то есть квадратом. Отрезок, соединяющий центр О с центром любой из четырех окружностей равен половине диагонали этого квадрата.
То есть ОВ = (1/2)*(2*R1)*√2= R1*√2. (1)
ОВ = R+R1 (2). Приравняем (1) и (2): R1*√2 = R+R1 =>
R1 = R/(√2 -1). Тогда площадь одного из внешних кругов равна
S = πR1² = πR²/(√2 -1)². Это ответ.
Если принять приближенное значение π ≈ 3,14, а √2 ≈ 1,41 то S ≈ 18,47*R² ед².
Приложения:
Автор ответа:
0
В ответе не дописал R² ! то есть S = 18,5R²
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Русский язык,
автор: alenakondratuk5130
Предмет: Физика,
автор: dimonnikakos
Предмет: Алгебра,
автор: sneg22