Предмет: Алгебра,
автор: llucifercute
Решить неравенство


Ответы
Автор ответа:
1
Ответ на фото////////////////
Приложения:
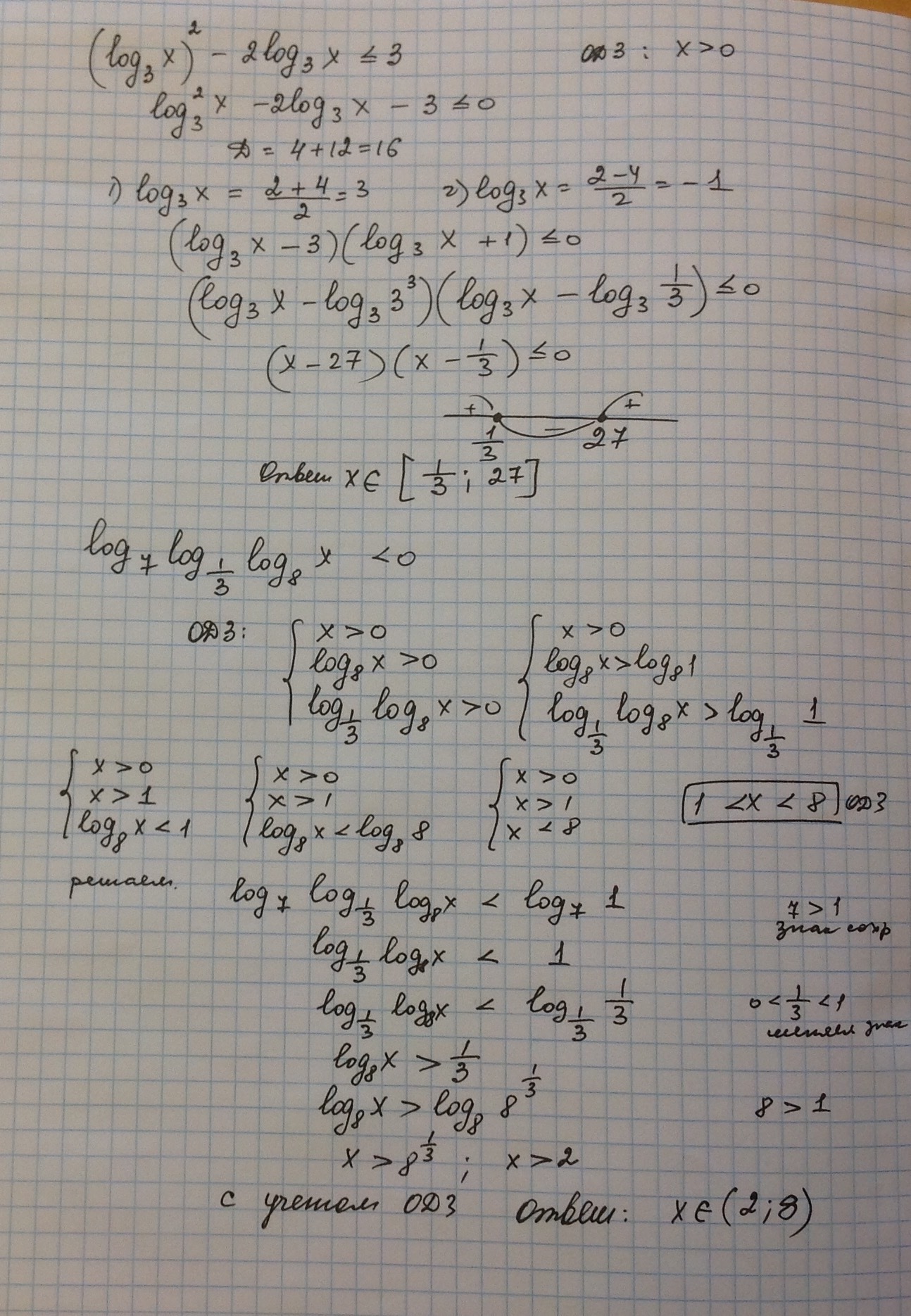
Автор ответа:
0
NNNLLL54:
31550968 - вопрос удалён
Похожие вопросы
Предмет: Геометрия,
автор: kakasha078
Предмет: Биология,
автор: nessikmay
Предмет: Алгебра,
автор: patyosyauchiha
Предмет: Математика,
автор: narbellik