Предмет: Алгебра,
автор: Nasta2548
Найти неопределенный интеграл и проверить результат дифференцированием
Приложения:
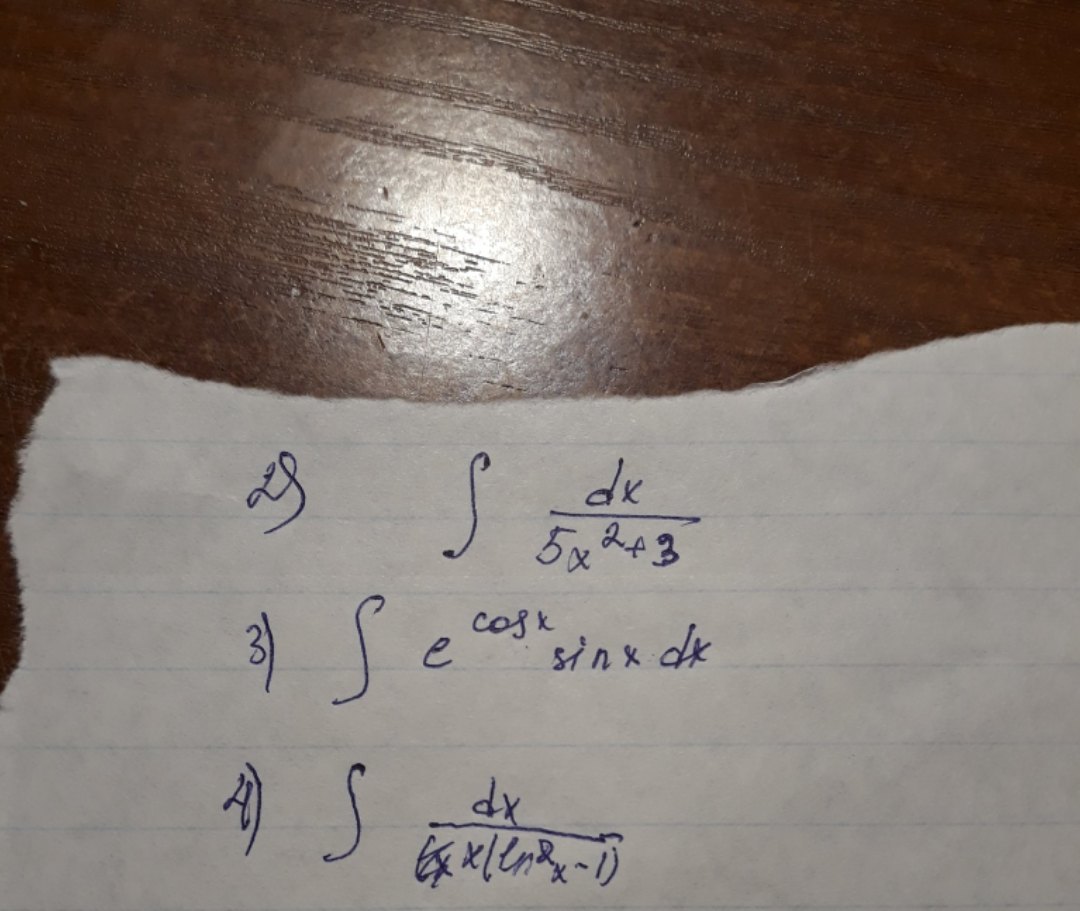
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: annasitn6982
Предмет: Геометрия,
автор: annettaandrushuk
Предмет: География,
автор: demamaslov2007
Предмет: Математика,
автор: zNeADeKVaTz
Предмет: Обществознание,
автор: Аноним