Предмет: Алгебра,
автор: svetlanazola
Решите уравнениеcos x + 2cos(2x-pi/3)=sqrt3 sin2x-1
Приложения:
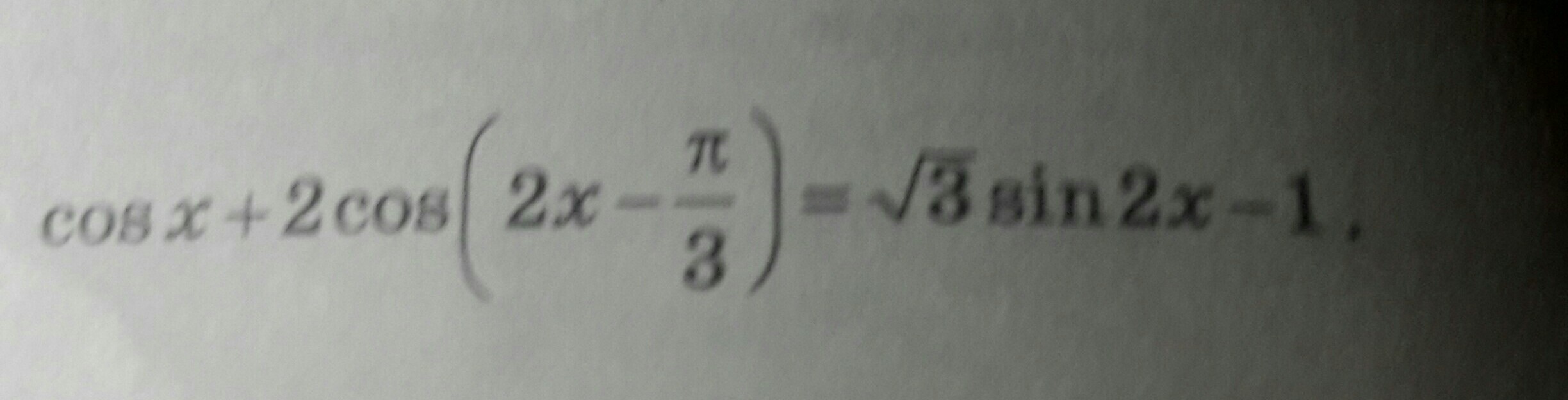
Ответы
Автор ответа:
26
Распишем второй косинус из левой части уравнения, как косинус разности двух аргументов.
Упростим.
Воспользуемся формулой косинуса двойного аргумента: cos2α = 2cos²α-1
Решим простейшие тригонометрические уравнения.
- ответ.
Похожие вопросы
Предмет: Математика,
автор: lidachorna1988
Предмет: Алгебра,
автор: maria9002
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: чума5
Предмет: Физика,
автор: лиза1648