Предмет: Геометрия,
автор: srty82
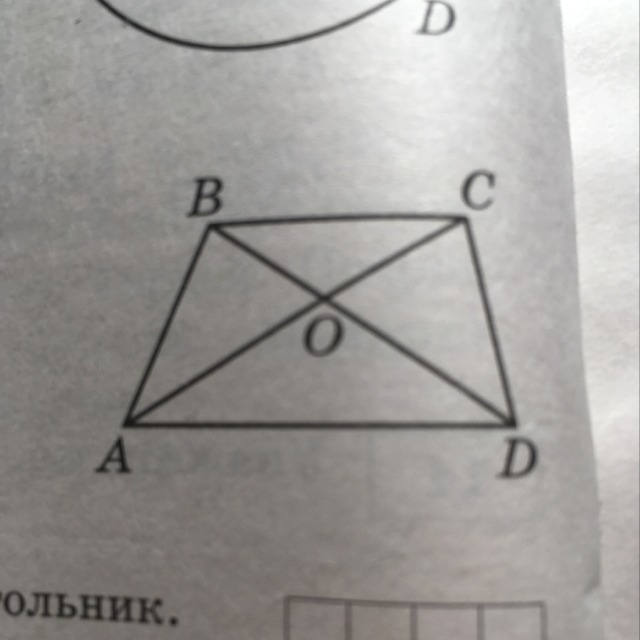
Диагонали AC и ВД трапеции ABCD с основаниями BC и АД пересекаются в точке О, ВС=9, АД=15, АС=16. Найдите СО
Приложения:
Ответы
Автор ответа:
1
Ответ:
СО=6
Объяснение:
Диагонали трапеции пересекаясь образуют 2 подобных треугольника ВОС и АОД. Поэтому их стороны будут взаимно пропорциональны:
Сократим дробь 9/15 на 3 и получим 3/5
Обозначим числитель и знаменатель 3х и 5х - это 2 части из которых состоит диагональ АС. Зная, что АС=16, составим уравнение:
3х+5х=16
8х=16
х=16÷8=2
Тогда АО=5×2=10, а СО=3×2=6
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: hhhhhhshssffa
Предмет: Математика,
автор: sertdemirasmin860
Предмет: Русский язык,
автор: ilasakupov57
Предмет: Математика,
автор: ali671
Предмет: Литература,
автор: kouovaiova