Предмет: Геометрия, автор: Аноним

Две стороны треугольника abc равны 5 и 8 см, угол между ними 120 градусов, найдите третью сторону
Срочно

Ответы

Автор ответа: 5tgb03

теорема косинусов

x - третья сторона

x^2 = 5^2 +8^2 -2*5*8*cos120 = 25+64-80*(-0,5) = 25+64+40 = 129

x = √ 129 см

5tgb03: три стороны треугольника
a = 5 см; b = 8 см; с = ?
угол между a и b 120 град
формула косинусов
c^2 = a^2 +b^2 - 2 a b cos(120)
^2 во второй степени
c^2 = 5^2 +8^2 - 2 *5 *8 * (-1/2) = 25 +64 +40 = 129
c = √129 см
ответ
третья сторона √129 см

Автор ответа: Hrisula

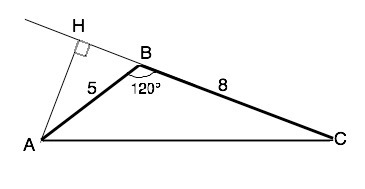
Вариант решения. Пусть данный треугольник АВС, АВ=5, ВС=8, угол АВС=120°. АН - высота из острого угла (в тупоугольном треугольнике лежит вне его). Угол АВН=60°, как смежный углу 120°. Тогда АН=AB•sin60°=5•(√3/2)=2,5√3 см, BH=AB•cos60°=5•1/2=2,5 см. Отсюда СН=ВН+ВС=10,5 см. По т.Пифагора АС=√(AH²+CH²)=√[(2√3)²+(10,5)²]= √129 см.