Question

Помогите, пожалуйста.
Не могу понять, как решать.
Обе задачи к одному рисунку.

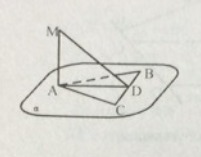
1) Дано: MA ⊥ (ABC)
AB = AC, CD = BD
Доказать:
MD ⊥ BC

2) Дано: MA ⊥ (ABC)
BC = CD, MD ⊥ BC
Доказать:
AB = AC

Answer 1

Объяснение:      

  1) Дано: MA ⊥ (ABC)

AB = AC, CD = BD

Доказать:

MD ⊥ BC

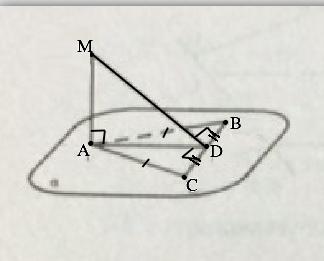
 ∆ АВС - равнобедренный (дано). СD=DB , => AD не только  медианаЭ но и высота равнобедренного треугольника, => AD⊥СВ.  

 МD - наклонная, АD  - ее проекция на плоскость АВС. => по т. о 3-х перпендикулярах  МD⊥ВС

-------------------------

      2) Дано: MA ⊥ (ABC)

BD = CD, MD ⊥ BC

Доказать:

AB = AC

 Наклонная MD ⊥ BC, => по т. о 3-х перпендикулярах ее проекция AD⊥ВС, следовательно,  AD - высота ∆ ВАС. Поскольку по условию BD = CD, отрезок АD - медиана ∆ ВАС. Если в треугольнике высота является его медианой, этот треугольник - равнобедренный. => AB = AC