Question

На рисунке ABCD- квадрат со стороной 6 см. Вычислите площадь пятиугольника AFBCD.

Answer 1

См. Фото

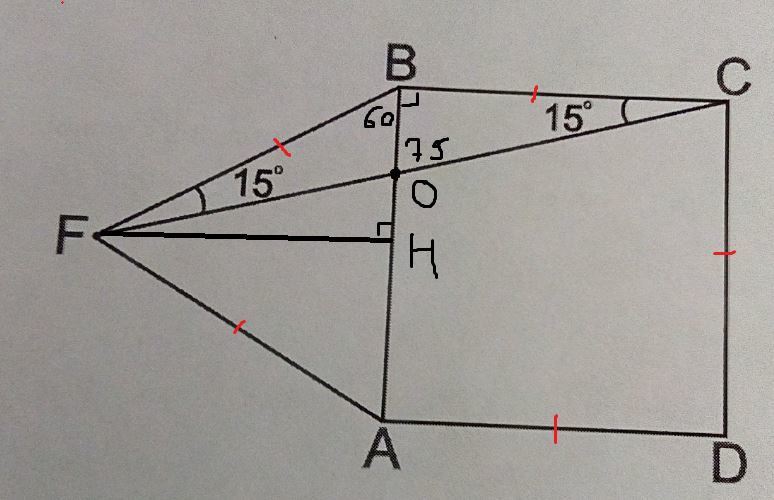
Пересечение BA и FC  пусть будет O

FBC равнобедренный ⇒ FB=BC=6

Внешний угол треугольника равен сумме двух не смежных с ним. В ΔFBO внешний - ∠BOC который равен 90°-15°=75°

Он равен ∠BFO+∠FBO

Тогда FBO=75°-∠BFO=60° и FB=BA ⇒ ΔFBA правильный

Проведём высоту FH (H на AB)

Тогда HF по т. пифагора= $\sqrt{6^{2}- 3^{2} } =\sqrt{27}$

S ΔFAB = FH*BA/2=(√27)*6/2=3√27=9√3

S abcd=36

Общая площадь = 36+9√3

Answer 2

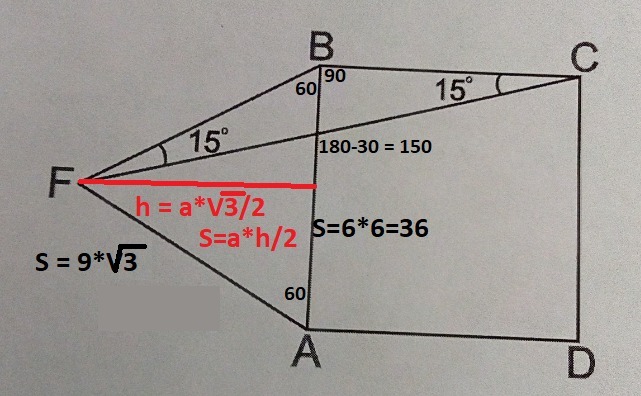
Ответ: 36 + 9√3 см² - площадь.

Пошаговое объяснение:

Сумма углов треугольника 180 градусов.

Получаем равносторонний треугольник ABF с углами в 60°.

Sin60° = √3/2. Площадь треугольника по формуле: S = a*h/2.