Предмет: Алгебра,
автор: kamilla2301
Номер 784 под цифрой (1,3) помогите решить,пожалуйста
Приложения:

Ответы
Автор ответа:
0
Вот решение твоих примеров:
Приложения:
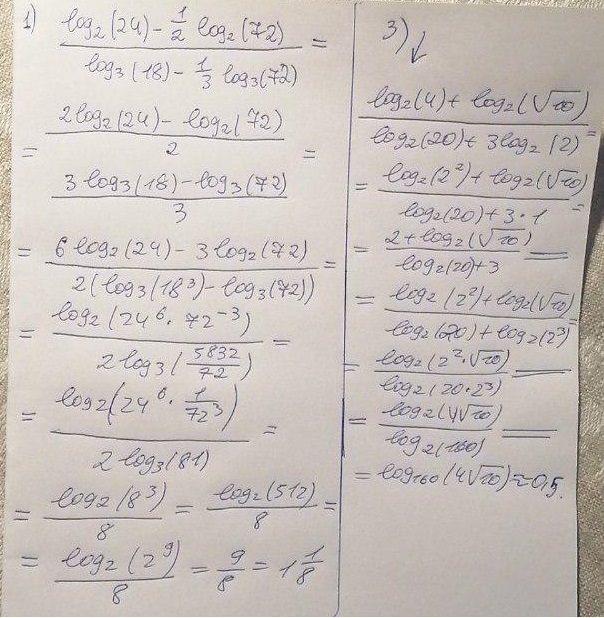
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: askarikcom
Предмет: Українська література,
автор: artem2285436
Предмет: Математика,
автор: alenapriadka2303
Предмет: Математика,
автор: Школотрол51
Предмет: Литература,
автор: Внриника