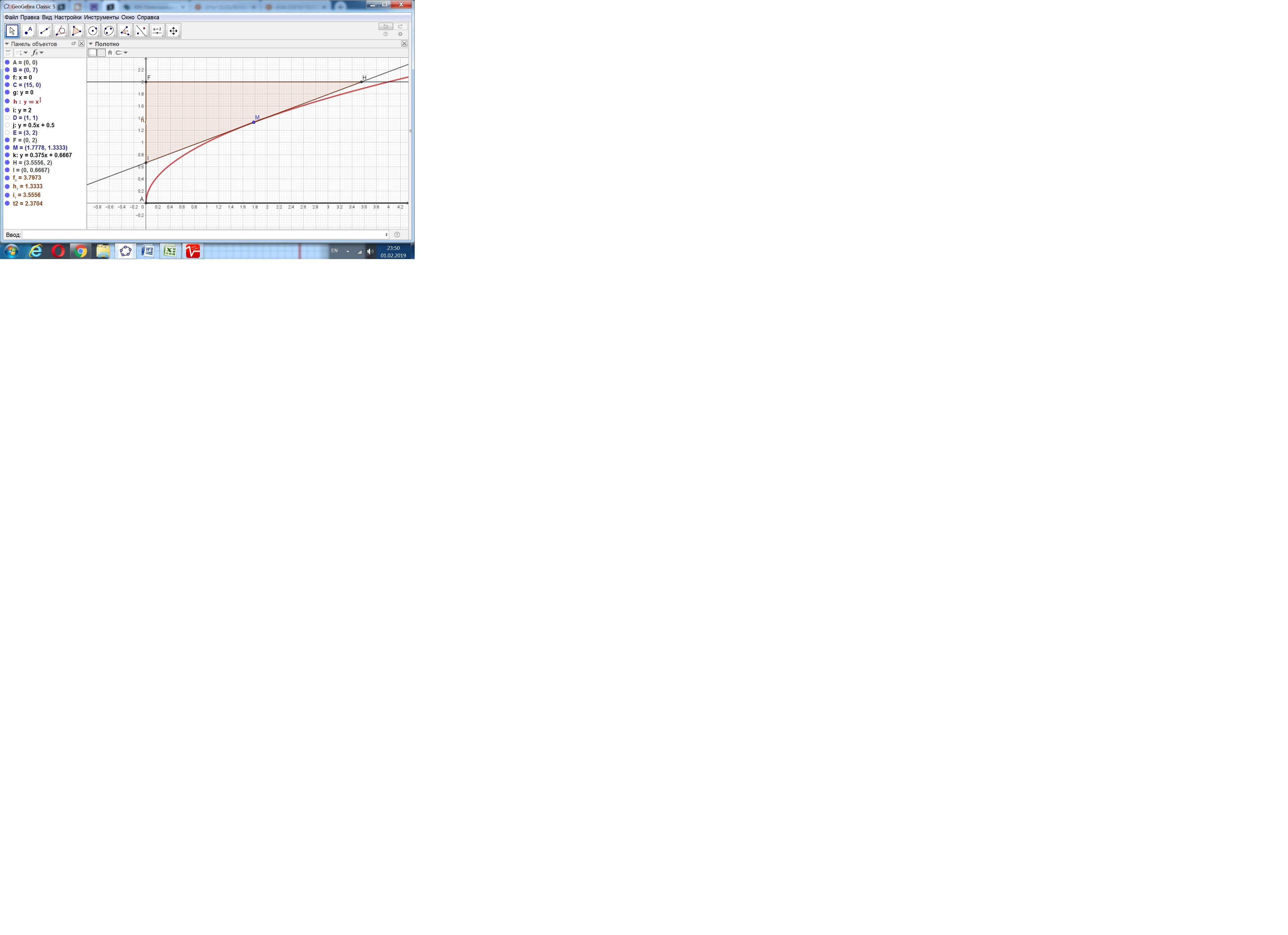
Фигура ограничена графиком функции (y=sqrt(x)),прямой (y=2) и осью ординат. В какой точке графика функции (y=sqrt(2)) (0 <= x <= 4 ) нужно провести касательную, чтобы она отсекала от указанной фигуры треугольник наибольшей площади?

Ответы
Касательная к графику функции у = √х имеет угловой коэффициент, равный производной функции: y' = 1/(2√x).
Примем уравнение в виде у = кх + в, где х и у - координаты точки касания. Вместо у подставим √x и получим значение отрезка в, отсекаемой касательной на оси Оу.
√x = (1/(2√x))*х + в. Отсюда получаем в = √x/2.
Теперь переходим к треугольнику, образованному этой касательной, осью ординат и прямой у = 2. Его катеты a b равны:
a = 2 - в = 2 - (√x/2) = (4 - √x)/2 и b = a/tgα = ((4 - √x)/2)/(1/(2√x)) =
= 4√x - x. Здесь tgα - это угловой коэффициент касательной, равный её производной. Площадь треугольника равна:
S = (1/2)*((4 - √x)/2)* (4√x - x) = (16√x - 8x + х√x)/4.
Производная площади равна S' = (3x + 16 - 16√x)/8√x.
Приравняем её нулю (достаточно числитель), используя замену √x = t.
Решаем уравнение 3*t^2-16*t+16=0.
Ищем дискриминант:
D=(-16)^2-4*3*16=256-4*3*16=256-12*16=256-192=64;
Дискриминант больше 0, уравнение имеет 2 корня:
t_1=(√64-(-16))/(2*3)=(8-(-16))/(2*3)=(8+16)/(2*3)=24/(2*3)=24/6=4;
t_2=(-√64-(-16))/(2*3)=(-8-(-16))/(2*3)=(-8+16)/(2*3)=8/(2*3)=8/6=4/3.
Обратная замена: х = t². x1 = 16 (не принимаем по ОДЗ), х2 = 16/9.
Это и есть ответ: х = (16/9).