помогите пожалуйста
Ответы
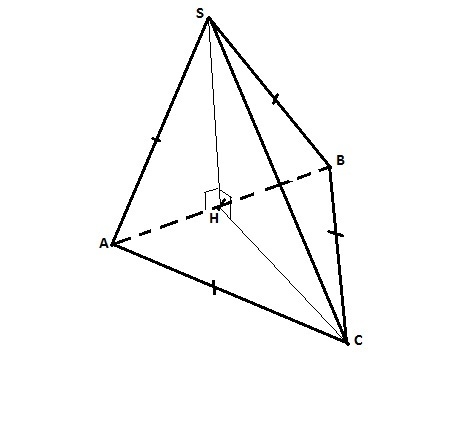
Площадь боковой поверхности данной пирамиды - сумма боковой поверхности трех боковых граней. Одна грань - правильный треугольник со стороной а=√(√15-√3) = √3(√5-1), а две другие - равные равнобедренные треугольники с боковыми сторонами, равными "а". По приложенному рисунку:
Sasb = (√3/4)*a - площадь правильного треугольника.
Заметим, что высоты боковой грани ASB и основания АВС равны между собой (правильные треугольники со стороной "а"). Найдем эти высоты (SH и СН) по формуле H=(√3/2)*a. или
Н=√(а²-SC²/4)=a√10/4. Тогда в равнобедренном прямоугольном треугольнике SHC гипотенуза
SC = (√3/2)*a*√2. Площадь боковой грани ASC равна
Sasc=(1/2)*SC*H или
Sasc=(1/2)*(√6/2)*a*(a√10)/4 = a²√60/16.
Sбок = Sasb+2*Sasc = (√3/4)a²+2*(a²√60)/16 = a²(2√3+√60)/8 или
Sбок= √3(√5-1)*(2√3+√60)/8 = 3*(√5-1)*2(1+√5)/8 = 6*(5-1)/8 =3 ед².