Question

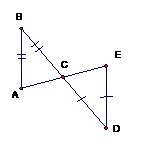
Докажите что AB II DE

Answer 1

Рассмотрим прямые AB, DE и секущую AE:
Угол BAC и угол DEC - накрест лежащие.
Докажем, что эти углы равны.
1) угол BCA = угол DCE (вертикальные)
2) угол BAC = угол BCA (в равнобедренном треугольнике углы при основании равны)
3) угол DCE = угол DEC (в равнобедренном треугольнике углы при основании равны)

1 |
2 |
3 |=> угол BAC = угол DEC => по признаку параллельности прямых AB||DE.