Question

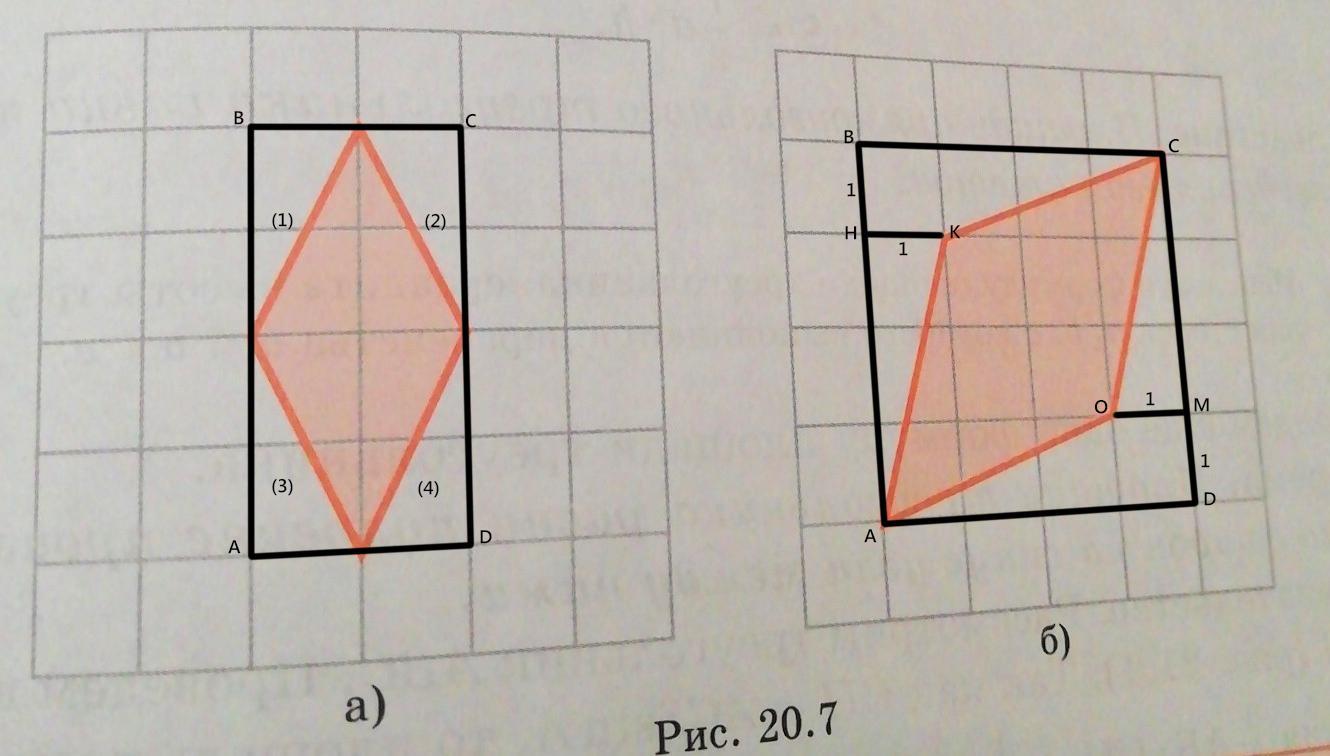
найдите площади четырехугольников изображенных на рисунке 20.7

Answer 1

Найдите площади четырехугольников изображенных на рисунке 20.7, приняв сторону клетки за 1 (ед.)

а)

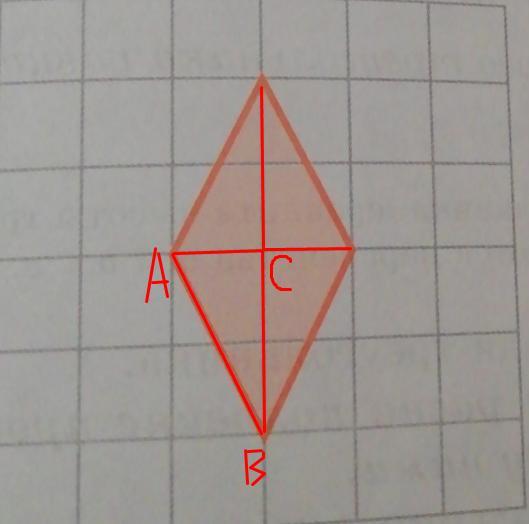
Рассмотрим выделенный мною (см. в приложении) треугольник, который я обозначил, как ABC. Он прямоугольный.

$\displaystyle S = \frac{1}{2} a * b$, где а и b  - катеты треугольника

Тогда S(ABC) = 1 * 2 : 2 = 1 (ед².)

Заметим, что предложенный четырехугольник состоит из 4 треугольников, равных треугольнику ABC.

Тогда:

S(искомая) = 4 * 1 = 4 ед²

Ответ: 4 ед²

b)

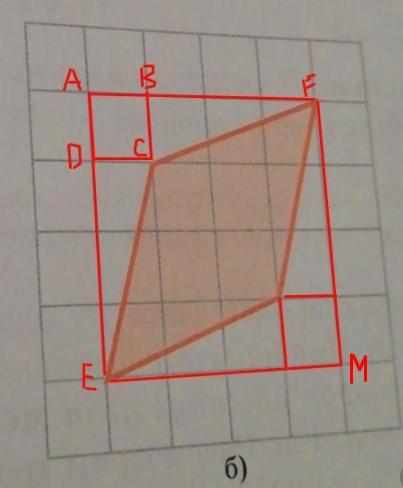
Найдем площадь квадрата AFME, обозначенного мною (см. в приложении № 2)

S = a² = 4² = 16 (ед.²)

Площадь квадрата ABCD:

S = 1 * 1 = 1 (ед.²)

Площадь треугольника BCF, по формуле, указанной выше:

S ΔBCF = 3 * 1 : 2 = 1,5 (ед.²)

ΔBCF = ΔDCE

Площади этих трех фигур - ΔBCF, ΔDCE и квадрата ABCD обтекают искомый четырехугольник в составе квадрата AFME. Совместная их площадь равна площади, обтекаемых фигур снизу. Таким образом искомая площадь равна:

S = 16 - (1 + 1.5 * 2) * 2 = 16 - 4 * 2 = 16 - 8 = 8 (ед.²)

Ответ: 8 (ед.²)

Answer 2

а)

Проведём дополнительные отрезки и обозначим вершины как показано на рисунке (смотрите в приложении).

Многоугольники, обозначенные цифрами 1, 2, 3, 4 - прямоугольные треугольники.

• Площадь прямоугольного треугольника равна половине произведения его катетов.

S₁ = 0,5*2*1 = 1 (ед²)

S₂ = 0,5*2*1 = 1 (ед²)

S₃ = 0,5*2*1 = 1 (ед²)

S₄ = 0,5*2*1 = 1 (ед²)

• Площадь прямоугольника равна произведению его двух смежных сторон.

Следовательно -

S(ABCD) = АВ*ВС = 4*2 = 8 (ед²).

S(ABCD) = S(оранжевой фигуры) + S₁ + S₂ + S₃ + S₄

S(оранжевой фигуры) = S(ABCD) - S₁ - S₂ - S₃ - S₄ = 8 (ед²) - 1 (ед²) - 1 (ед²) - 1 (ед²) - 1 (ед²) = 4 (ед²).

Ответ :

4 (ед²).

- - -

б)

Также проводим дополнительные отрезки и обозначаем вершины.

Фигуры AHK и COM - прямоугольные треугольники.

S(ΔAHK) = 0,5*3*1 = 1,5 (ед²)

S(ΔCOM) =  0,5*3*1 = 1,5 (ед²).

Фигуры КНВС и ОМDA - трапеции (причём прямоугольные).

• Площадь трапеции равна произведению полусуммы его оснований и высоты.

S(КНВС) = 0,5*(ВС + НК)*ВН = 0,5*(4 + 1)*1 = 0,5*5*1 = 2,5 (ед²)

S(ОМDA) = 0,5*(AD + OM)*MD = 0,5*(4 + 1)*1 = 0,5*5*1 = 2,5 (ед²)

S(ABCD) = АВ*ВС = 4*4 = 16 (ед²).

S(ABCD) = S(оранжевой фигуры) + S(ΔAHK) + S(ΔCOM) + S(КНВС) + S(ОМDA)

S(оранжевой фигуры) = S(ABCD) - S(ΔAHK) - S(ΔCOM) - S(КНВС) - S(ОМDA) = 16 (ед²) - 1,5 (ед²) - 1,5 (ед²) - 2,5 (ед²) - 2,5 (ед²)  = 8 (ед²).

Ответ :

8 (ед²).