Предмет: Алгебра,
автор: Garrathol
Интегрирование способом подстановки.
2 примера.
70 баллов.
Очень нужно решить.
Приложения:
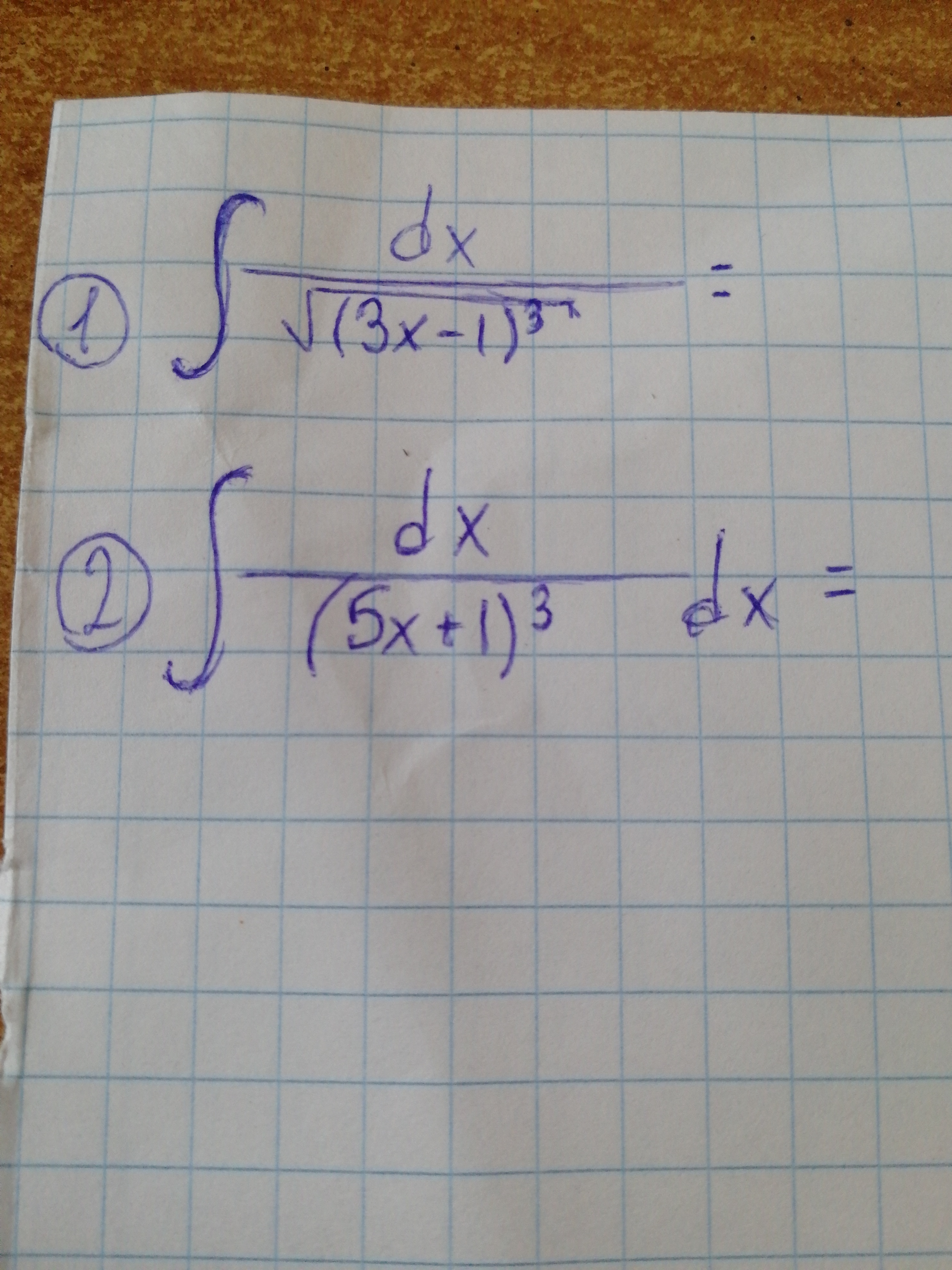
LFP:
3x-1 = t... 3dx = dt... интеграл от t в степени -(3/2) *3 dt... обычный степенной интеграл))
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Русский язык,
автор: guzun1404200999
Предмет: Геометрия,
автор: starovoytmaks
Предмет: Математика,
автор: andrijgumen34
Предмет: Математика,
автор: хадижат951
Предмет: Геометрия,
автор: masha456789