Предмет: Алгебра,
автор: Аноним
помогите решить один интеграл
Приложения:
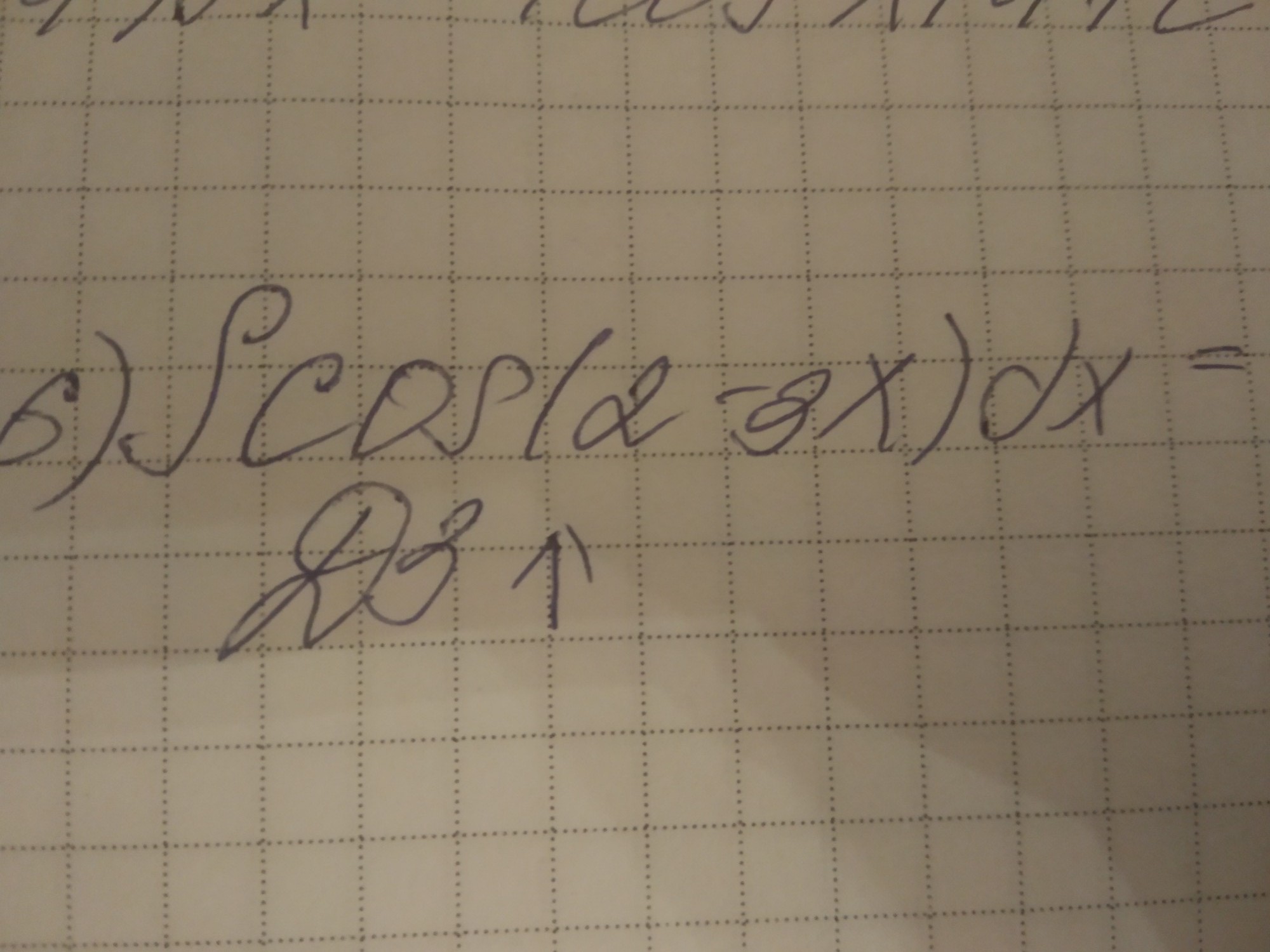
Ответы
Автор ответа:
3
Обозначим t = 2-3x ⇒ x = (2 - t)/3
Найдём дифференциал dx
Теперь наш интеграл будет выглядеть так
Вернём замену:
Ответ:
Похожие вопросы
Предмет: Математика,
автор: sailonbs21
Предмет: Физика,
автор: ira2393
Предмет: Химия,
автор: ilon4ik5
Предмет: Математика,
автор: fgdgfsy