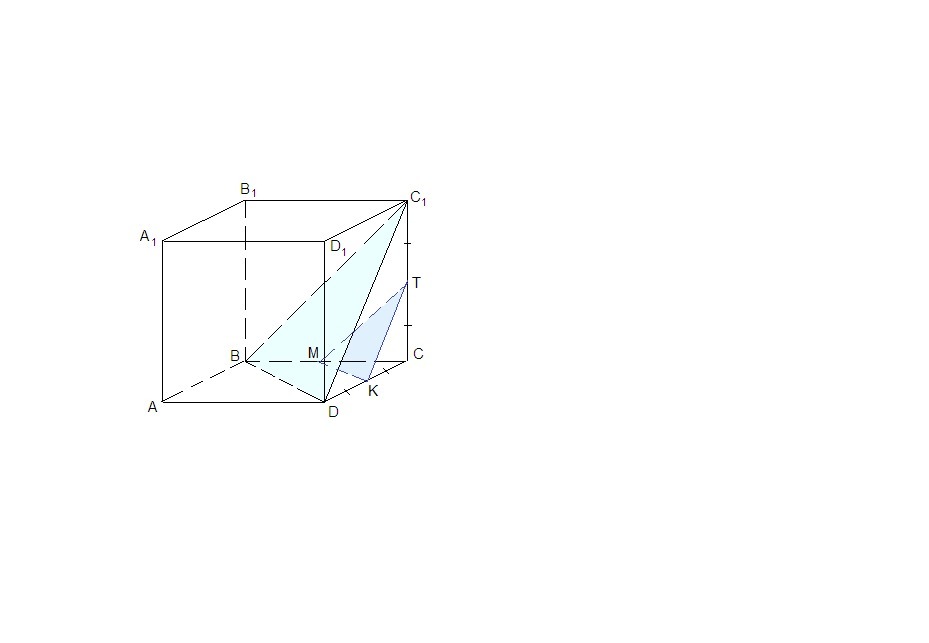
Пункт T - середина канта CC1 куба ABCDA1B1C1D1. Постройте сечение куба плоскостью, которая проходит через пункт T и паралельна плоскости BC1 . Найдите площадь поверхности куба, если площадь полученного сечения равна 4√3 см2.
Прошу решение с рисунком.
Ответы
Рисунок в принципе можно развернуть, так получится более красивее)

В условии опечатка: надо построить сечение куба плоскостью, параллельной плоскости ВС1D.
Точки В, С₁ и D лежат попарно в одинаковых гранях. Соединим их. Получим равносторонний треугольник (все стороны являются диагоналями равных квадратов).
Отметим точки М - середину ВС, и К - середину CD. Соединим их и точку Т.
ТМ║С₁В как средняя линия ΔС₁СВ,
ТК║С₁D как средняя линия ΔС₁СD, значит плоскость ТКМ параллельна плоскости ВС₁D, значит ТКМ - искомое сечение.
Так как стороны треугольника ТКМ равны половинам сторон треугольника ВС₁D как средние линии соответствующих треугольников, то ТКМ так же равносторонний. Его площадь:
Stkm = TM²√3/4
TM²√3 / 4 = 4√3
TM² = 16
TM = 4 cм
ВС₁ = 2ТМ = 8 см - диагональ грани куба.
Площадь квадрата можно найти по формуле:
S = d²/2 (квадрат - тот же ромб, площадь равна половине произведения диагоналей, а у квадрата диагонали равны)
S = 8² / 2 = 64/2 = 32 см²
Площадь поверхности куба:
Sпов = 6 · 32 = 192 см²