найдите точки экстремума функции и значения функции в точках экстремума
у=х^4-2х^2
Ответы
y = x⁴ - 2x²
Чтобы найти экстремумы, для начала нам нужно найти производную, а потом приравнять её к нулю, решив уравнение:
y' = (x⁴ - 2x²)' = (x⁴)' - (2x²)' = 4 · x⁴⁻¹ - 2 · 2 · x²⁻¹ = 4x³ - 4x
y' = 0, тогда:
4x³ - 4x = 0
4x · (x² - 1) = 0 в том случае, когда:
1. 4x = 0
x = 0
2. x² - 1 = 0
x² = 1
x = ± 1
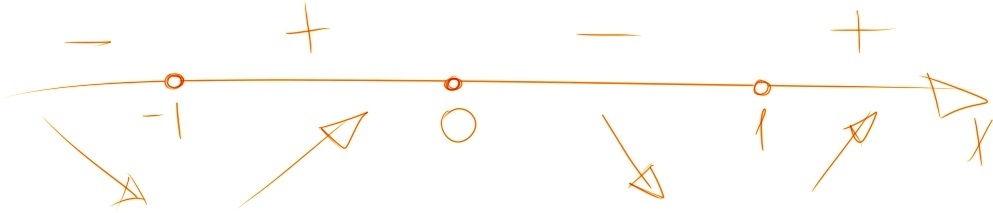
Проведём числовую прямую и по методу интервалов определим, на каких промежутках значение функции положительно, а где отрицательно:
(смотри рисунок)
Чтобы определить знак функции на определённом промежутке, нужно подставить какое-то значение из этого промежутка в производную.
Точки экстремума - это точки максимума и минимума. Точка максимума - это точка, до которой график функции возрастал, а после этой точки убывал. Точка минимум - наоборот. На нашей числовой прямой таких экстремумов 3:
- x₁ = -1 (минимум)
- x₂ = 0 (максимум)
- x₃ = 1 (минимум)
Найдём значение функции в этих точках:
- y(x₁) = x₁⁴ - 2x₁² = 1 - 2 = -1
- y(x₂) = x₂⁴ - 2x₂² = 0
- y(x₃) = x₃⁴ - 2x₃² = 1 - 2 = -1