Предмет: Математика,
автор: ivankoledov2001
Помогите пожалуйста решить уравнение
Приложения:
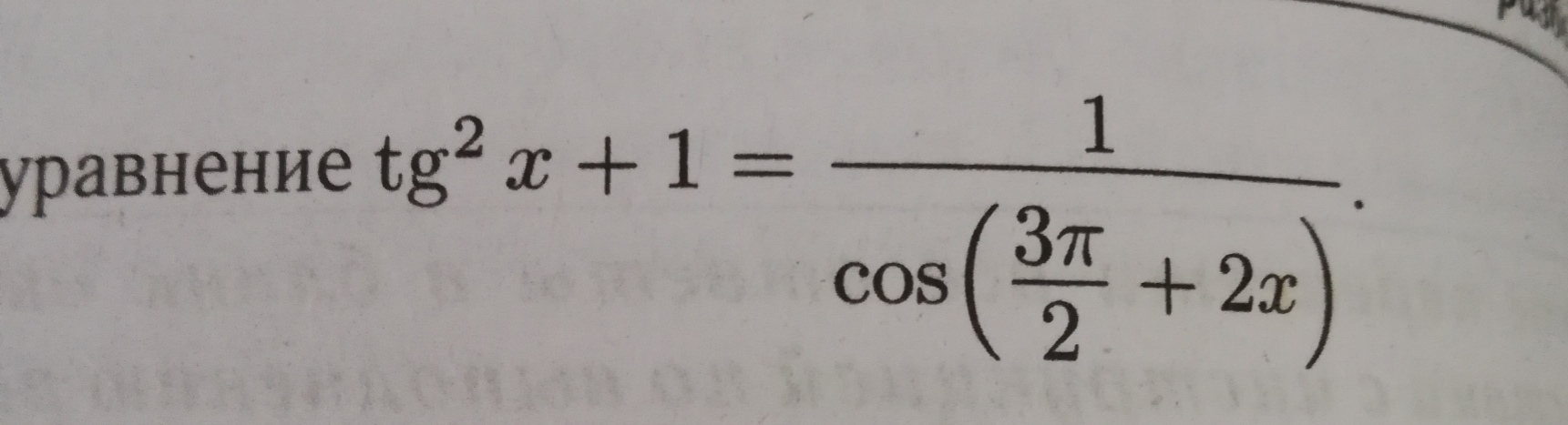
Ответы
Автор ответа:
0
Ответ:
Решение
Тригонометрическая подстановка t=tgx/2
И ответ)
ганж:
Где видишь А с шапочкой не обращай на нее внимание, это в программе я случайно пробел наверно поставил)
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: n3008334
Предмет: Русский язык,
автор: leetelefon
Предмет: Математика,
автор: ислам217
Предмет: Геометрия,
автор: nechepurenko02