Дети создали цели в виде правильного треугольника, в которые стреляют пластмассовыми шариками (смотрите изображение). Все треугольники правильные.
Какова вероятность попасть в шестиугольник. Какова вероятность попасть в один из темно-серых треугольников?
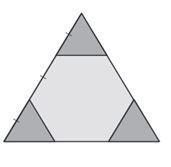
Ответы
Ответ:
2/3 ; 1/3
Пошаговое объяснение:
Вероятность попадания в маленький треугольник или в шестиугольник определяется площадью соответствующих фигур. Квалификация и желание стрелков, а также вероятность промаха в условии не заданы. Считается только попадание в тот или другой участок фигуры, общая вероятность попадания в фигуру принята в данном случае за 1
Поскольку учитывается попадание в любой из маленьких треугольников, то имеет значение общая площадь всех трех.
а ---- сторона 6-ти угольника и маленького равностороннего треугольника
S₆ = (3а²√3)/2 ---- площадь правильного 6-ти угольника со стороной а
S₃ = (а²√3)/4 ----площадь равностороннего треугольника, построенного на стороне 6-ти угольника а
3S₃ = (3а²√3)/4 ----- общая площадь трех треугольников
S = (3а²√3)/2 + (3а²√3)/4 = (9а²√3)/4 ---- общая площадь фигуры-мишени
р₆ = S₆/S = ((3а²√3)/2) / ((9а²√3)/4) = 2/3 ----- вероятность попадания в шестиугольник
р₃ = ((3а²√3)/4) / (9а²√3)/4) = 1/3 ---- вероятность попадания в один из маленьких темных треугольников
Ответ: 2/3 и 1/3