Question

Диагонали трапеции равны 10 см и 12 см. Найдите периметр четырёхугольника, вершинами которого являются середины сторон данной трапеции.

Answer 1

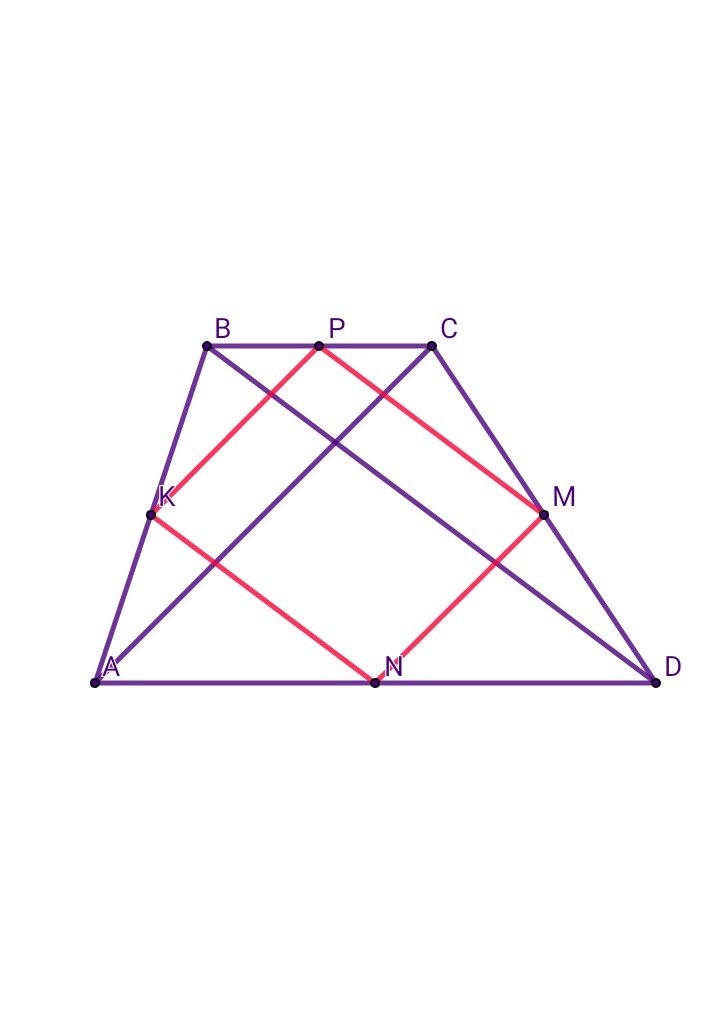
Пусть К, Р, M, N - середины сторон соответственно АВ, BC, CD, AD, тогда

В ΔABD: AK = KB, AN = ND ⇒ KN - средняя линия

" Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны "

KN || BD, KN = BD/2

В ΔBCD: BP = PC, CM = MD ⇒ PM - средняя линия

PM || BD, PM = BD/2

Значит, KN || PM , KN = PM

Из этого следует, что четырёхугольник KPMN - параллелограмм (по признаку параллелограмма)

KN = BD/2 , KP = AC/2

Р kpmn = 2•(KN + KP) = 2•(BD/2 + AC/2) = BD + AC = 12 + 10 = 22 см

ОТВЕТ: Р = 22 см