Question

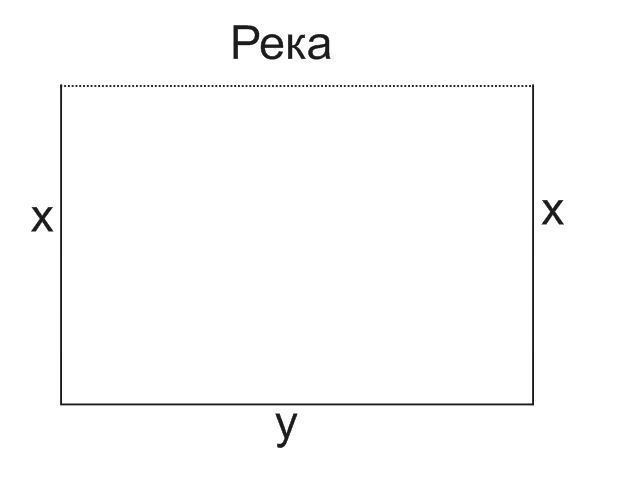
Забором длиной 80 метров нужно ограничить участок земли прямоугольной формы, одна сторона которого, совпадает с берегом реки(У береги реки забор не строится). Определите стороны прямоугольника так, чтобы площадь была наибольший.

Answer 1

Ответ:

S= 400 м^2

Пошаговое объяснение:

X - длина

P = (a+b)*2

(80-2x):2 - ширина ( Исходя из формулы выше. )

S = x(80-2x):2 = (x(80-2x)/2 = (x*2(40-x))/2=x(40-x) = 40x-x^2

s' = 40-2x (Точка максимума)

s' = 0 (Точка минимума)

0 = 40-2x

2x = 40

x = 20 метров.

Возвращаемся к формуле (80-2x):2 и ставим значение x.

(80-2*20):2=20(метров)

Длина равняется ширине, то есть это квадрат.

Получается, что максимальное значение площади при данных параметрах равняется 400 метрам квадратным

20*20= 400 м^2