СРОЧНО
Составить уравнение линии, все точки которой равноудаленны от прямой х=-2 и точки (4,0)
Ответы
Ответ:
Пошаговое объяснение:
Ответ на фото

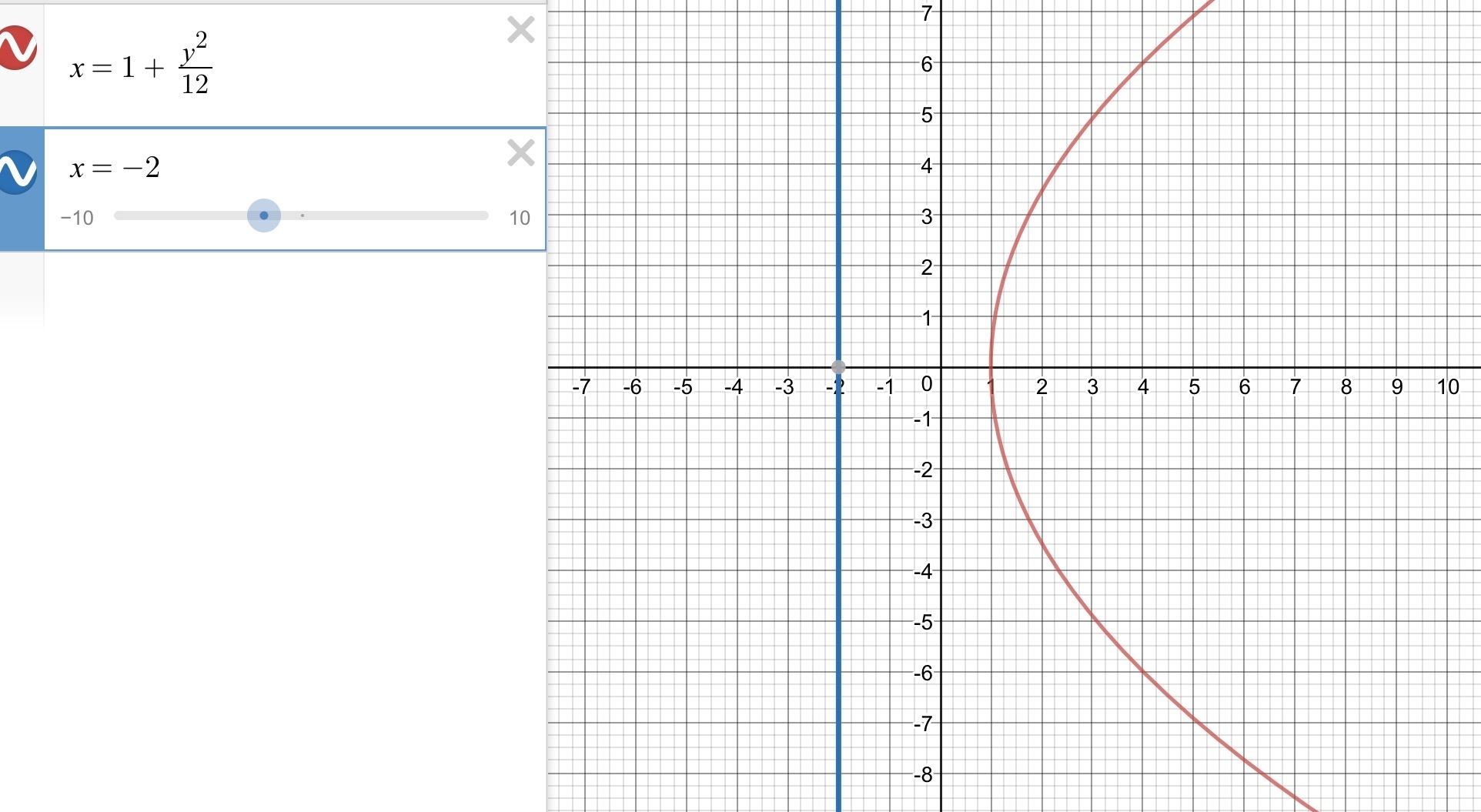
M(x,y) - точка на заданной линии.
Расстояние от точки М до прямой равно d и расстояние от точки М до точки F(4,0) равно d .
По формуле расстояния от точки до прямой находим
По формуле расстояния между двумя точками находим
Парабола с вершиной в точке (1,0) , ветви направлены вправо (значит фокус параболы находится правее вершины) .
. Фокус параболы находится в точке, удалённой от вершины на
единицы на оси ОХ, то есть ,в точке F(1+3,0)=(4,0) . Директриса параболы находится на таком же расстоянии от вершины в противоположную сторону, то есть уравнение директрисы: х=1-3 , х= -2 .
Замечание. Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой.