Предмет: Алгебра,
автор: Аноним
решите пожалуйста очень срочно нужно
Приложения:
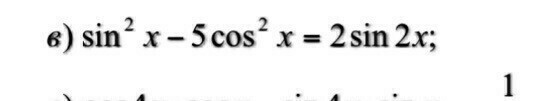
Ответы
Автор ответа:
1
sin²x - 5cos²x = 2sin2x
sin2x = 2sinx•cosx - синус двойного аргумента
sin²x - 4sinx•cosx - 5cos²x = 0
Разделим обе части данного уравнения на cos²x ≠ 0, тогда
(sin²x/cos²x) - (4sinx•cosx/cos²x) - (5cos²x/cos²x) = 0
tg²x - 4tgx - 5 = 0
Пусть tgx = a, a ∈ R, тогда
a² - 4a - 5 = 0
D = (-4)² - 4•1•(-5) = 16 + 20 = 36
a₁ = (4 - 6)/2 = - 2/2 = - 1 ⇔ tgx = - 1 ⇔ x = (-π/4) + πn
a₂ = (4 + 6)/2 = 10/2 = 5 ⇔ tgx = 5 ⇔ x = arctg5 + πn, n ∈ Z
ОТВЕТ: (-π/4) + πn ; arctg5 + πn, n ∈ Z
Похожие вопросы
Предмет: Английский язык,
автор: procivroman19
Предмет: Математика,
автор: panddagame
Предмет: Информатика,
автор: Z005043mr
Предмет: Математика,
автор: LAPTENOK1
Предмет: Математика,
автор: 55555258