Предмет: Математика,
автор: Derzach
Мат анализ
Под номером 2 и 3
Найти производную методом логарифмического дифференцирования
Приложения:
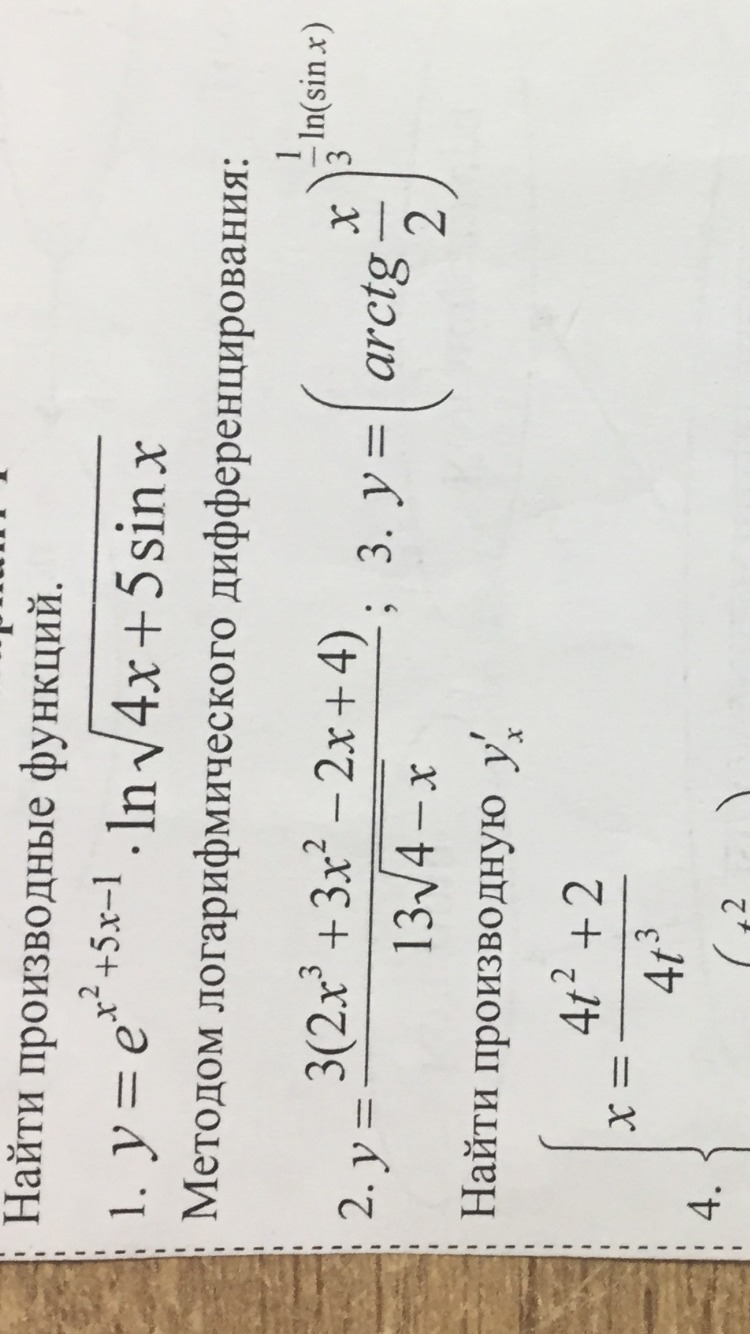
Ответы
Автор ответа:
1
Решение выполнено без подставления исходного значения вместо у.
Приложения:

Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: karapetana269
Предмет: Биология,
автор: Аноним
Предмет: Другие предметы,
автор: katavolosuk28
Предмет: Математика,
автор: nikita20072
Предмет: Литература,
автор: Наталия1988