Question

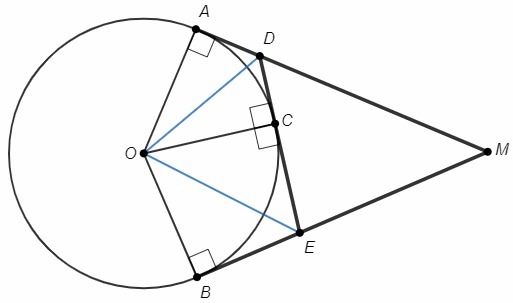
Помогите срочно, пожалуйста. Из точки М проведены к окружности с центром в точке О касательные МА и MB. Прямая l касается окружности в точке С и пересекает МА и MB соответственно в точках D и Е. Доказать, что: а) периметр треугольника MDE не зависит от выбора точки С; б) угол DOE не зависит от выбора точки С.

Answer 1

а) Отрезки касательных, проведенных из одной точки, равны.

DA=DC, EB=EC

P(MDE)= MD+DC+ME+EC =MD+DA+ME+EB =MA+MB

Кроме того, MA=MB => P(MDE)/2 =MA=MB  

б) Радиусы OA и OB перпендикулярны касательным. Сумма противоположных углов четырехугольника AOBM равна 180, ∠AOB+∠M=180. По свойству отрезков касательных из одной точки* OD - биссектриса ∠AOC, OE - биссектриса ∠BOC.

∠DOE= ∠AOC/2 +∠BOC/2 =∠AOB/2 =(180-∠M)/2

----------------------------

*△DOA=△DOC по катету (радиус) и общей гипотенузе, их соответствующие элементы равны. Аналогично △EOB=△EOC.