Question

решите неравенство:
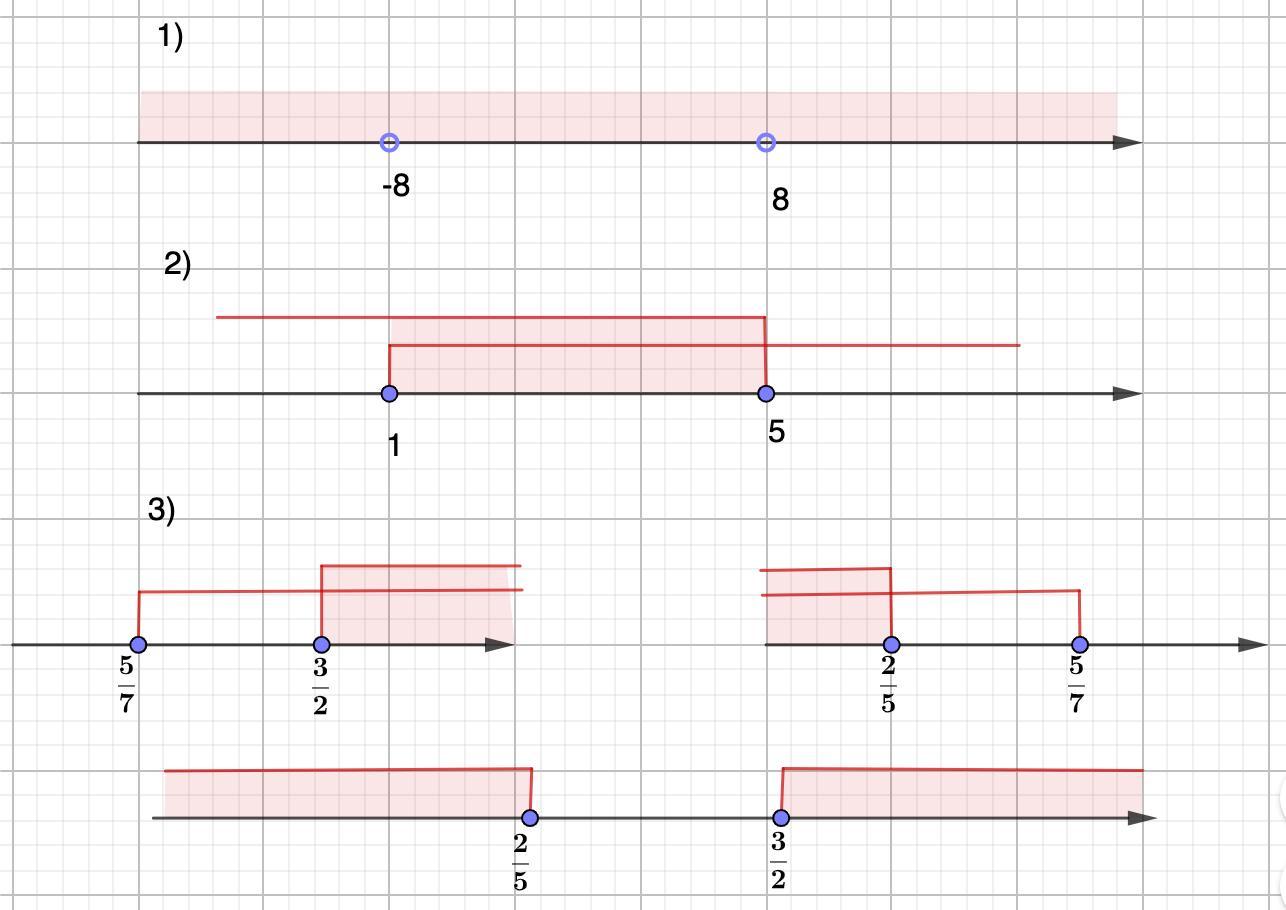
1)|x²-64|>0
2)|4x-12|≤8
3)|7x-5|≥3x+1

Answer 1

Объяснение:

1)

$\displaystyle |x^2-64|>0$

Модуль числа неотрицателен. Так у нас строгое неравенство, то его решением будут любые значения х кроме:

$\displaystyle x^2-64=0\\\\(x-8)(x+8)=0\\\\x=8;\;\;\;\;\;x=-8$

x ∈ (-∞;-8) ∪ (8;-8) ∪ (8;+∞)

2.

$\displaystyle |4x-12| \leq 8$

Данное неравенство равносильно системе:

$\displaystyle \left \{ {{4x-12\leq 8} \atop {-4x+12\leq 8}} \right. \;\;\;\left \{ {{4x\leq 20\;\;\;|:4} \atop {-4x\leq -4}\;\;\;|:(-4)} \right. \;\;\;\left \{ {{x\leq 5} \atop {x\geq 1}} \right.$

x ∈ [1; 5]

3.

$\displaystyle |7x-5|\geq 3x+1$

Данное неравенство равносильно совокупности двух систем:

$\displaystyle \left \{ {{7x-5\geq 0} \atop {7x-5\geq 3x+1 }} \right. \\\\\left \{ {{x\geq \frac{5}{7} } \atop {4x\geq 6}} \right. \\\\\left \{ {{x\geq \frac{5}{7} } \atop {x\geq \frac{3}{2} }} \right.$

$\displaystyle x\in[\frac{3}{2};+\infty )$

или

$\displaystyle \left \{ {{7x-5\leq 0} \atop {-7x+5\geq 3x+1}} \right. \\\\\left \{ {{x\leq \frac{5}{7} } \atop {-10x\geq -4}} \right. \\\\\left \{ {{x\leq \frac{5}{7} } \atop {x\leq \frac{2}{5} }} \right.$

$\displaystyle x\in(-\infty;\frac{2}{5}]$

Решением будет объединение всех решений.

$\displaystyle x\in(-\infty;\frac{2}{5}]\cup[\frac{3}{2};\infty} )$