Предмет: Алгебра,
автор: Aloner0509
Решите показательное уравнение:
Приложения:
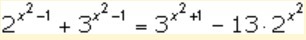
Ответы
Автор ответа:
1
Ответ:
Aloner0509:
скажите пожалуйста, а как у Вас получилось 27\2 в четвёртой строчке?
всё, понял, мы представили 13 на 26\2
Похожие вопросы
Предмет: Математика,
автор: 184izhikova3a
Предмет: Другие предметы,
автор: Aliona0192
Предмет: Литература,
автор: noelllove715
Предмет: Математика,
автор: Nafisa2005
Предмет: Математика,
автор: Бхй