Question

Помогите, пожалуйста. Надо решить задачу.

Answer 1

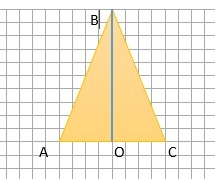
Пусть ABC - осевое сечение конуса. ВО- высота конуса. ∠АВС=60°.

Так как ΔABC - равнобедренный, ВО - медиана биссектриса, высота.

Значит ∠АВО=30°. ВО= 6. Пусть АО=х, тогда АВ=2х. (по свойству катета прямоугольного треугольника, лежащего против угла в 30° )

Тогда по теореме Пифагора

$(2*x)^{2} =x^{2} +6^{2} ; 4x^{2} -x^{2} =36; 3x^{2} =36; x^{2} =12; x=\sqrt{12} =2\sqrt{3}$

Следовательно, образующая равна АВ =2*2$\sqrt{3} =4\sqrt{3}$, радиус основания конуса равен АО= $2\sqrt{3}$

Площадь основания конуса равна $S=\pi r^{2} =\pi (2\sqrt{3} )^{2} =12\pi$

Ответ 12$\pi$; $4*\sqrt{3}$