Предмет: Алгебра,
автор: alinamak
Решить показательное неравенство: (1/3)^x+2+(1/3)^-x-3<=4
Ответы
Автор ответа:
7
Ответ на фото/////////////////
Приложения:
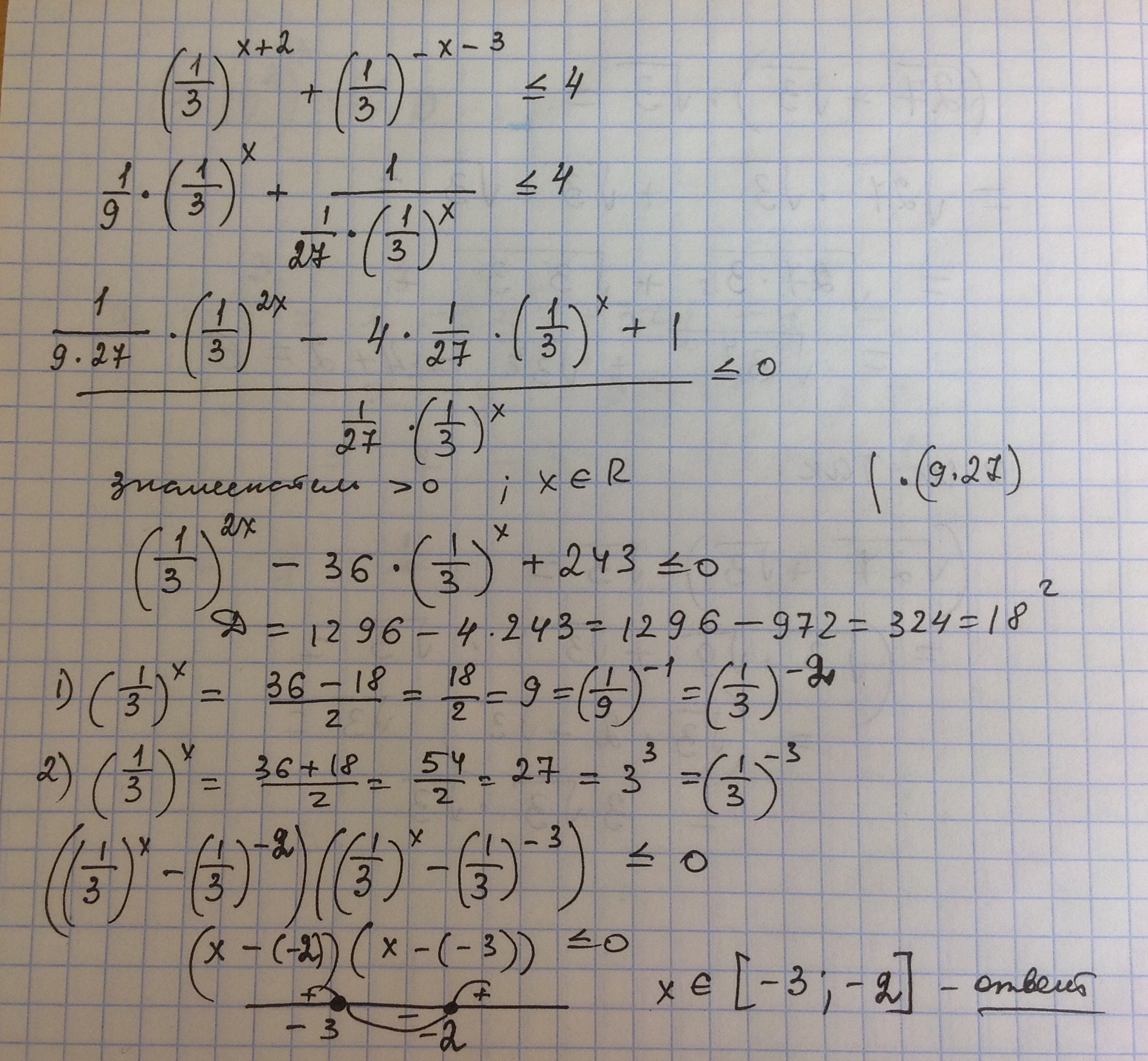
Автор ответа:
2
(1/3)^(x+2)+1/3^(-x-3)≤4
x€(-oo;+oo)
(1/3)^x *1/9+1/(1/3)x*(1/3)³≤4
(1/3)^x=t>0
t/9+27/t-4≤0
t²+243-36t≤0
t²-36t+243≤0
D1=324-243=81=9²
t=18±9
t1=27;t2=9
t€[9;27]
{(1/3)^x≤27;(1/3)^x≤(1/3)^(-3);x≥-3
{(1/3)^x≥9;(1/3)^x≥(1/3)^(-2);x≤-2
=>x€[-3;-2]
x€(-oo;+oo)
(1/3)^x *1/9+1/(1/3)x*(1/3)³≤4
(1/3)^x=t>0
t/9+27/t-4≤0
t²+243-36t≤0
t²-36t+243≤0
D1=324-243=81=9²
t=18±9
t1=27;t2=9
t€[9;27]
{(1/3)^x≤27;(1/3)^x≤(1/3)^(-3);x≥-3
{(1/3)^x≥9;(1/3)^x≥(1/3)^(-2);x≤-2
=>x€[-3;-2]
Похожие вопросы
Предмет: Физика,
автор: Nataljasidorova1467
Предмет: Русский язык,
автор: polinaivanova2510
Предмет: Физика,
автор: alenasv57
Предмет: История,
автор: NastyaGoldNya