Предмет: Математика,
автор: mc0mrade
Здравствуйте.Помогите найти пределы функций,не пользуясь правилом Лопиталя
Приложения:
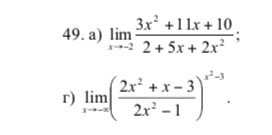
Ответы
Автор ответа:
2
Классика:
Похожие вопросы
Предмет: Геометрия,
автор: babnssa
Предмет: Русский язык,
автор: playmamba
Предмет: Информатика,
автор: andreymel009
Предмет: Математика,
автор: vlastilin003
Предмет: Литература,
автор: oksaloskutova