Question

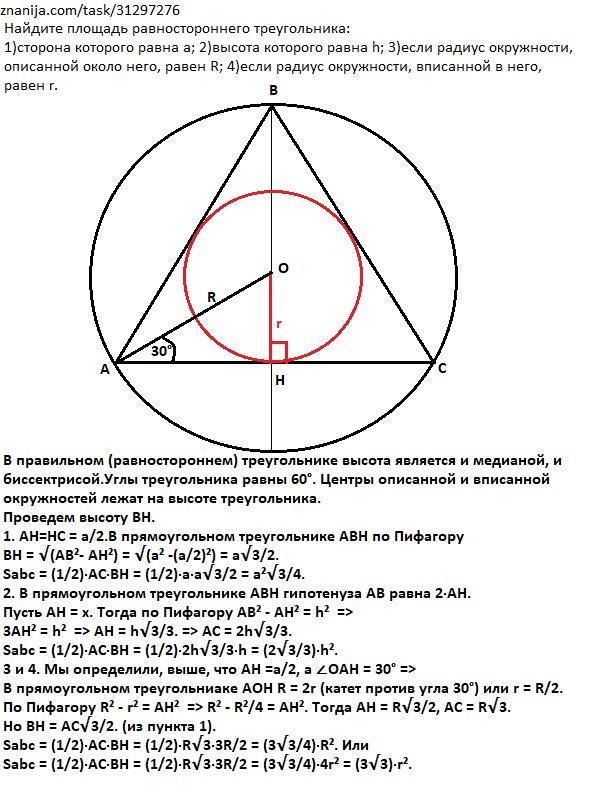
Найдите площадь равностороннего треугольника 1)сторона которого равна a; 2)высота которого равна h; 3)если радиус окружности, описанной около него, равен R; 4)если радиус окружности, вписанной в него, равен r.
ПОМОГИТЕ, ПОЖАЛУЙСТА !!!
ГЕОМЕТРИЯ!
10 БАЛЛОВ.

Answer 1

Ответ:

1. Sabc = (√3/4)·a².

2. Sabc = (2√3/3)·h².

3.  Sabc = (3√3/4)·R².

4.  Sabc = (3√3)·r².

Объяснение:

В правильном (равностороннем) треугольнике высота является и медианой, и биссектрисой.Углы треугольника равны 60°. Центры описанной и вписанной окружностей лежат на высоте треугольника.

Проведем высоту ВН.  

1. АН=НС = а/2.В прямоугольном треугольнике АВН по Пифагору  

ВН = √(АВ²- АН²) = √(а² -(a/2)²) = a√3/2.  

Sabc = (1/2)·AC·BH = (1/2)·a·a√3/2 = a²√3/4.

2. В прямоугольном треугольнике АВН гипотенуза АВ равна 2·АН.

Пусть АН = х. Тогда по Пифагору АВ² - АН² = h²  =>

3AH² = h²  => AH = h√3/3. => AC = 2h√3/3.

Sabc = (1/2)·AC·BH = (1/2)·2h√3/3·h = (2√3/3)·h².

3 и 4. Мы определили, выше, что АН =а/2, а ∠ОАН = 30° =>

В прямоугольном треугольнике АОН R = 2r (катет против угла 30°) или r = R/2.

По Пифагору R² - r² = AH²  => R² - R²/4 = AH². Тогда АН = R√3/2, АС = R√3.

Но ВН = АС√3/2. (из пункта 1).

Sabc = (1/2)·AC·BH = (1/2)·R√3·3R/2 = (3√3/4)·R². Или

Sabc = (1/2)·AC·BH = (1/2)·R√3·3R/2 = (3√3/4)·4r² = (3√3)·r².