Question

Провести полное исследование функции и построить график

Answer 1

Дано: y = x³/(x⁴+1)

Исследование.

1. Область определения. D(x)=R,  X∈(-∞;+∞).

2. Непрерывная, гладкая, разрывов - нет, вертикальных асимптот - нет.

3. Пересечение с осью ОХ -  нули функции. Y(x)= 0 при Х₁=0.

4. Пересечение с осью ОУ. Y(0) = 0.

5. Интервалы знакопостоянства.

Y(x)>0 при X∈(-∞;0] и Y(x)<0 при Х∈[0;+∞)

6. Проверка на чётность.

Y(-x) = - Y(x) -  функция нечётная.

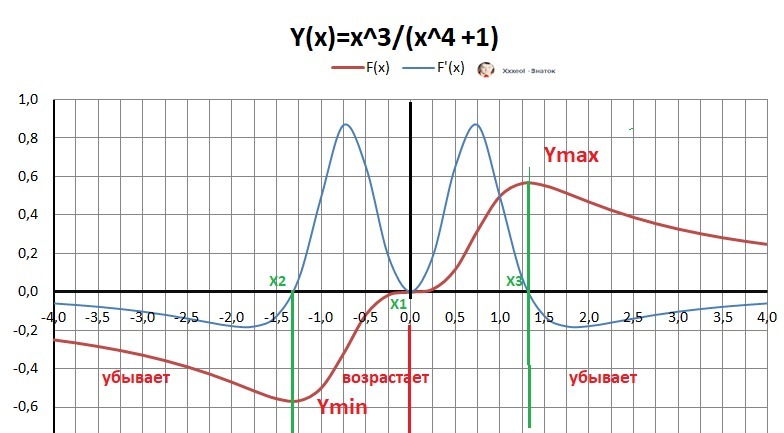
7. Поиск экстремумов по первой производной.

$Y'(x)=\frac{3x^2}{x^4+1}-\frac{4x^6}{(x^4+1)^2}=0$

Корни производной - локальные экстремумы -

X₂= -3¹/⁴ ≈-1 .32,  X₃=3¹/⁴ ≈ 1.32 (график на рисунке)

8. Локальные экстремумы.

Ymin(X₂)≈ -0.57 - минимум, Ymax(X₃) ≈ 0.57.

9. Интервалы монотонности.

Убывает: X∈(-∞;X₂]∪[X₃;+∞). Возрастает: X∈[X₂;X₃].

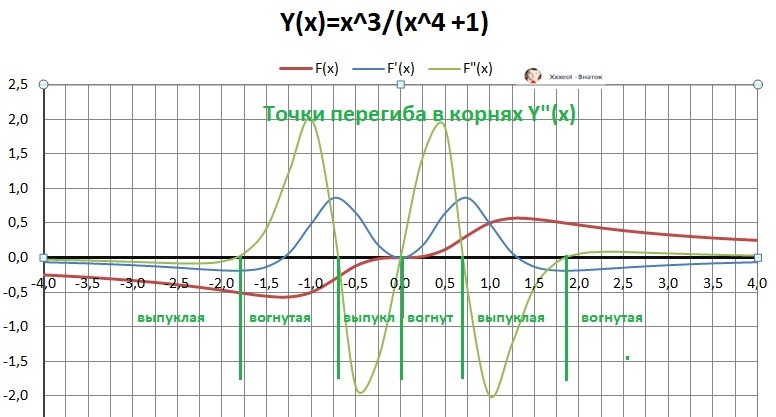
10. Поиск точек перегиба по второй производной.

$Y"(x)=\frac{6x}{x^4+1}-\frac{36x^5}{(x^4+1)^2}+\frac{32x^9}{(x^4+1)^3}=0$

(тихий ужас)

11. Значения точек перегиба не вычислить. Подробности на рисунке в приложении.

12. Горизонтальная асимптота.

k = lim(+∞) Y(x)/x = 0  Y = 0.

Y(-∞) = 0,  Y(+∞) = 0.

13. Область значений:  E(x) ≈ ± 0.57