Предмет: Алгебра,
автор: Fonimiko
Помогите решить, срочно!
Приложения:
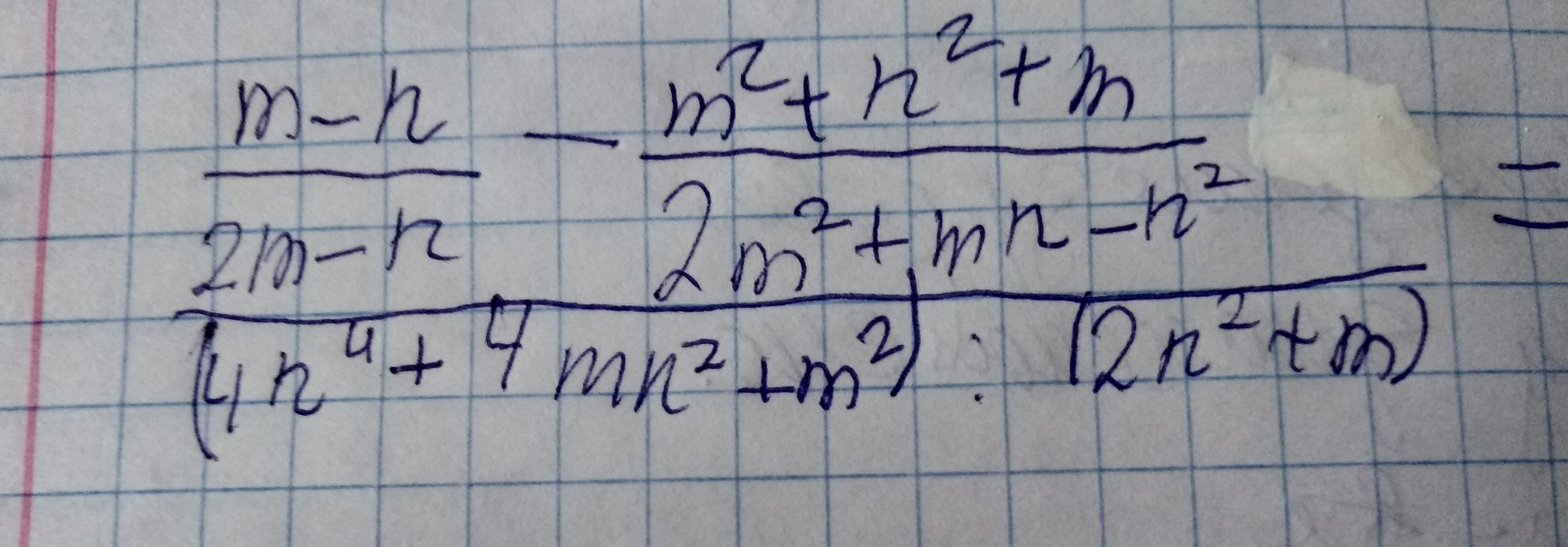
Ответы
Автор ответа:
1
Fonimiko:
Спасибо огромное!
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: saturn72926
Предмет: Математика,
автор: milana5254
Предмет: Математика,
автор: ВиНиПуХ1337
Предмет: Математика,
автор: FOOTBAL34