Предмет: Математика,
автор: liska1303
Определить область сходимости ряда:
Приложения:
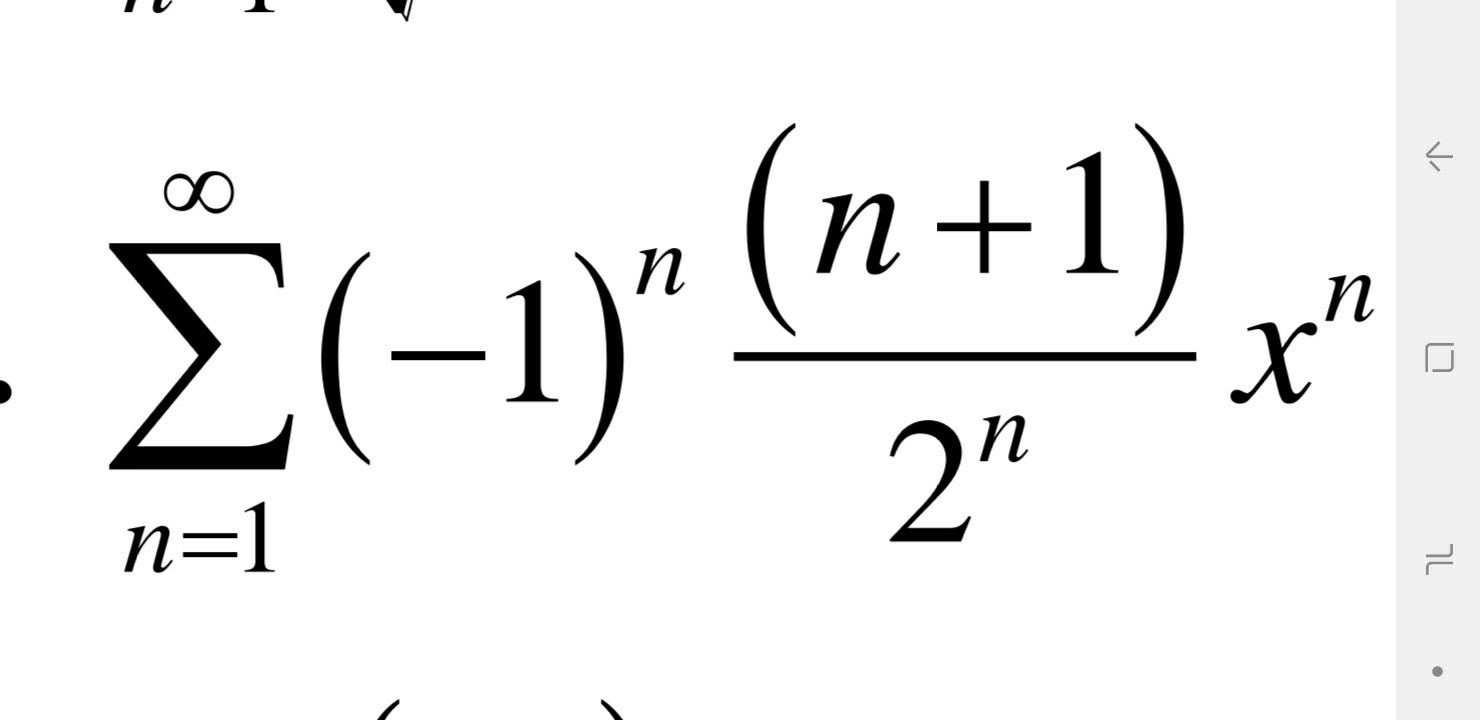
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:

Автор ответа:
1
Воспользуемся признаком Д'Аламбера.
Мы нашли интервал сходимости. А теперь самое "вкусное": исследует тот бардак,что получается на границах:
Ряд расходится, так как не выполняется условие ни абсолютной ни условной сходимости.
Ряд расходится согласно необходимого признака сходимости.
Ответ: -2<x<2
Похожие вопросы
Предмет: Геометрия,
автор: hinatasoe012
Предмет: Українська мова,
автор: hiynablude
Предмет: Українська література,
автор: handrex127
Предмет: Математика,
автор: 123ANUTA123