Предмет: Математика,
автор: mirdrujbajvachka
Вычислить производные:
а) степенно-показательной функции
б) неявно заданной функции
в) параметрически заданной функции
Приложения:
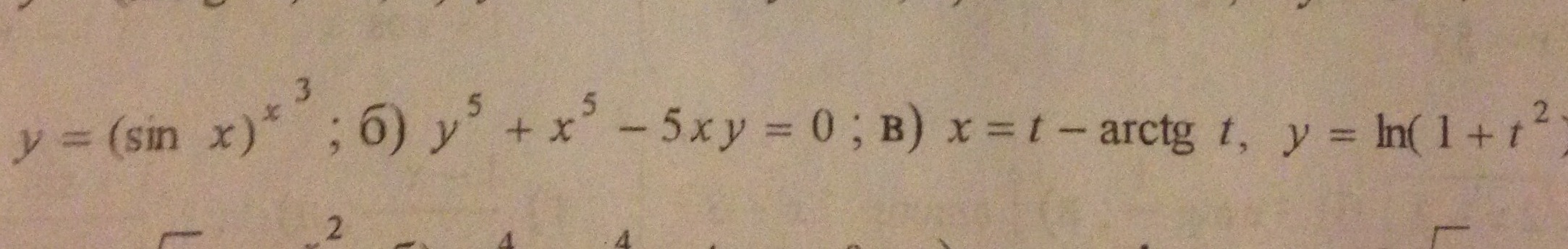
Ответы
Автор ответа:
1
а)
б)
в)
ivnv12:
В примере в перепутан числитель и знаменатель: y'/x'
Да, это так, отправьте жалобу на неправильный ответ
может проще исправить?
у меня не доступно это меню
Похожие вопросы
Предмет: Геометрия,
автор: FoksterKR
Предмет: Математика,
автор: imberikthe18
Предмет: Биология,
автор: hugsjojolove
Предмет: Математика,
автор: dula2
Предмет: Химия,
автор: mia33