Предмет: Алгебра,
автор: Pelio
Помогите решить тригонометрическое уравнение (желательно с подробным решением):
2cos2x+sin3x=2
Ответы
Автор ответа:
1
2*cos(2x)+sin(3x)=2
sin(3x)=2-2*cos(2x)
sin(3x)=4*sin^2(x)
Формула: sin(3x)=3*sin(x)-4*sin^3(x)
3*sin(x)-4*sin^3(x)=4*sin^2(x)
4*sin^3(x)+4*sin^2(x)-3*sin(x)=0
sin(x)*(4*sin^2(x)+4*sin(x)-3)=0
sin(x)=0 4*sin^2(x)+4*sin(x)-3=0
x=π*k, k - целое D=16+48=64
sin(x)=1/2 sin(x)= -3/2
x=π/6+2πk нет решений
x=5π/6+2πk
Ответ: x=π*k; x=π/6+2πk; x=5π/6+2πk , k - целое
Автор ответа:
1
sin3x=3sinx -4sin^3 x
Приложения:
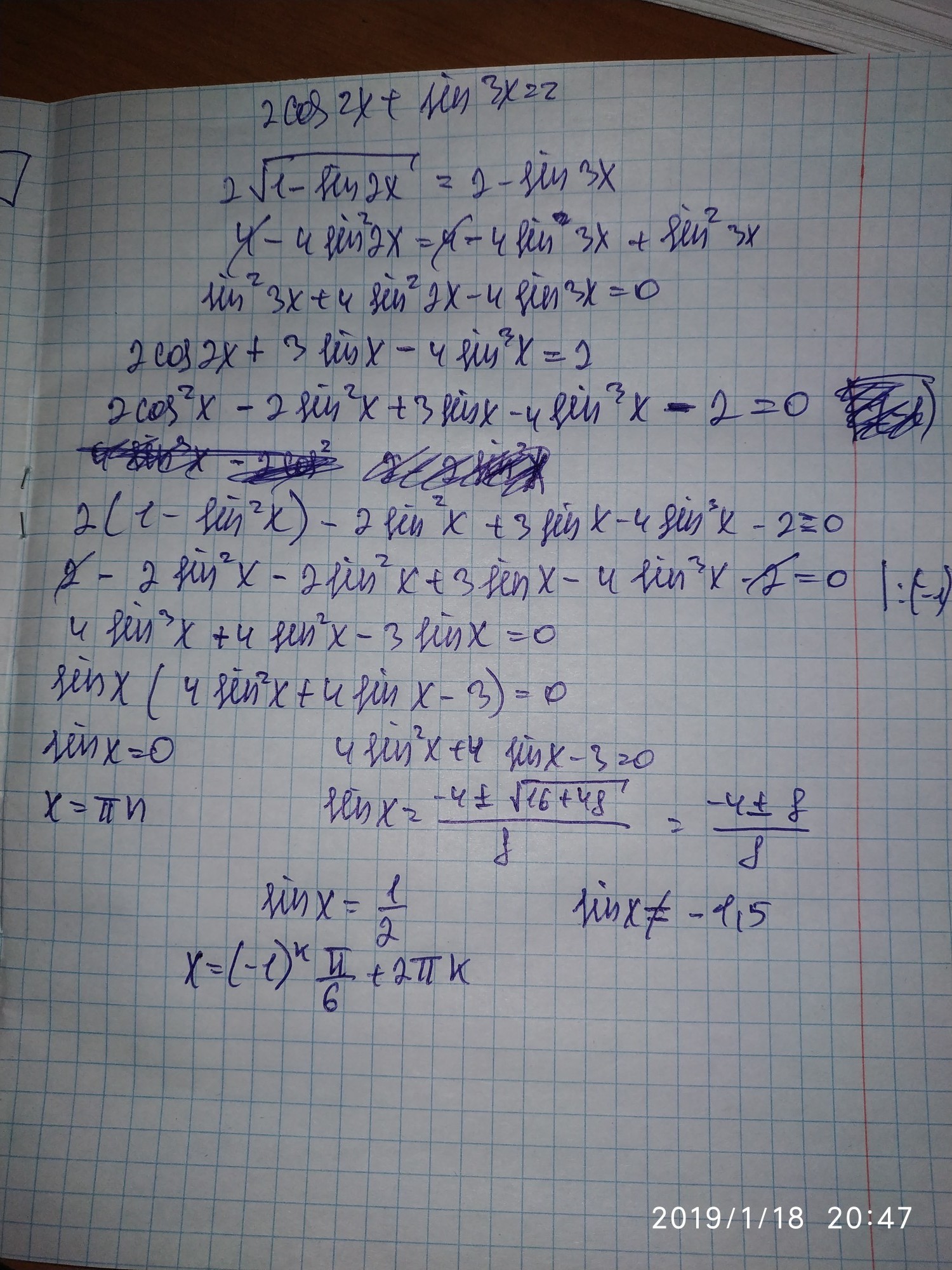
Похожие вопросы
Предмет: Математика,
автор: migitkos2012
Предмет: Математика,
автор: princessaafsana
Предмет: Другие предметы,
автор: qabdyshongar
Предмет: Биология,
автор: nastiayurievna
Предмет: История,
автор: NelyaMyrr22