Предмет: Алгебра,
автор: krancevicbsi
Помогите решить пожалуйстa
Приложения:
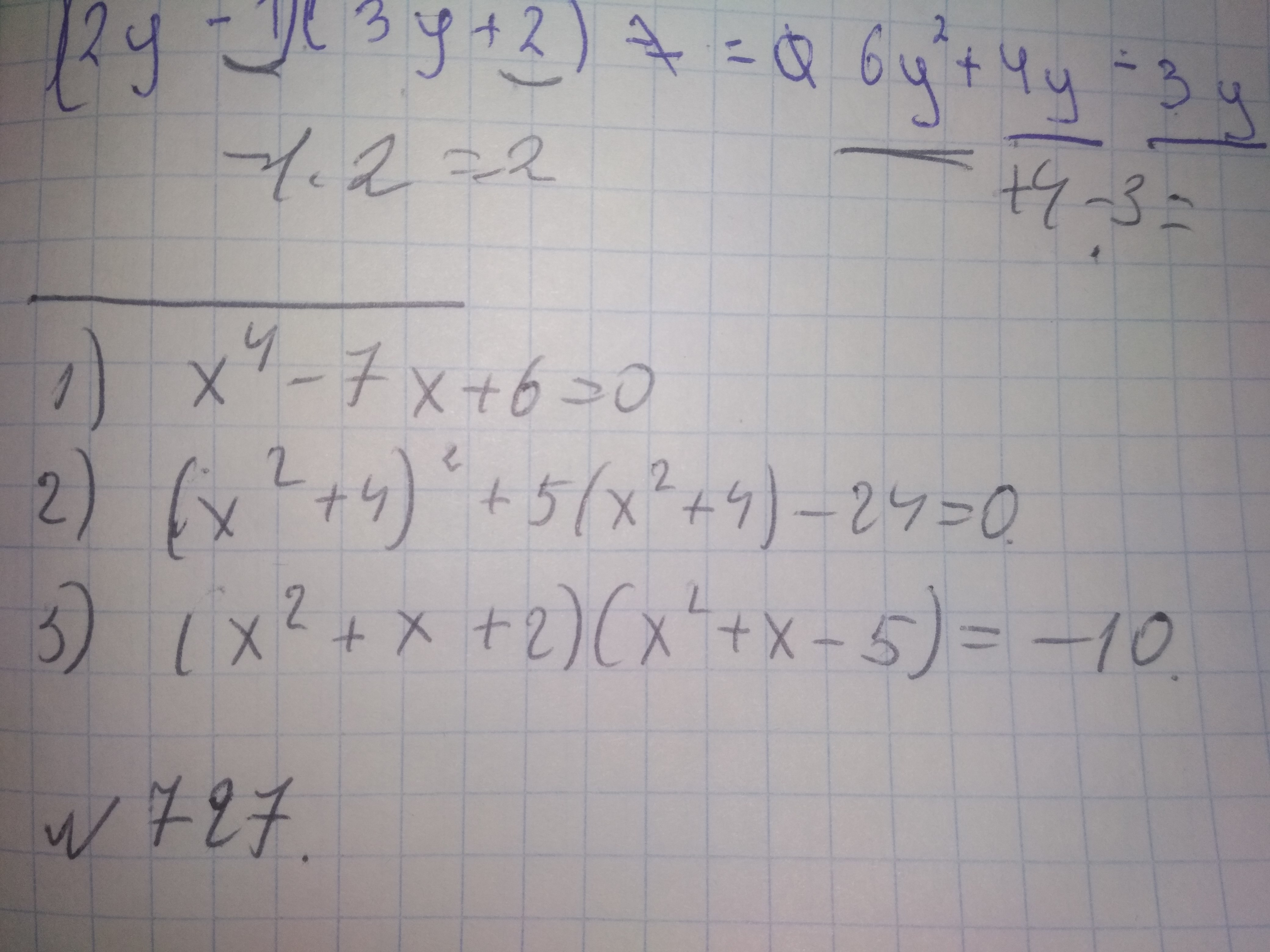
Dushzhanov987:
может быть там x^4 -7x^2 +6=0?
Нет
подбором можно решить, получится 1 корень x=1, остальные корни будут комплексными.
Ответы
Автор ответа:
1
Ответ: корней нет
Ответ:
Похожие вопросы
Предмет: Физика,
автор: ajdynkyzysynar4
Предмет: Биология,
автор: gmasloviev
Предмет: Геометрия,
автор: lioiaibatullina
Предмет: Математика,
автор: Zoyan
Предмет: География,
автор: 990Наташа990