Предмет: Геометрия,
автор: adeptus5731
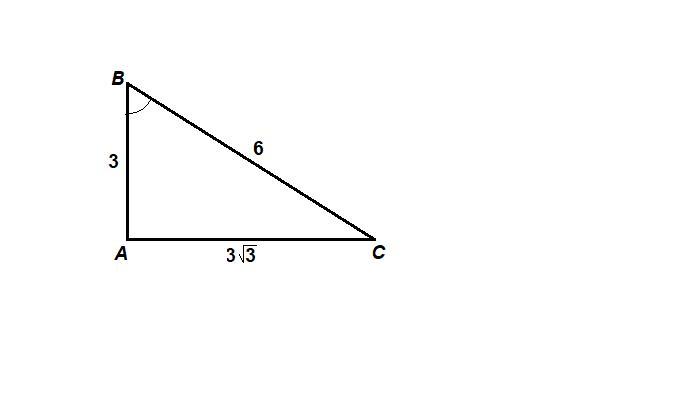
В треугольнике ABC Ac=3 корня из3,АВ=3,ВС=6.Найти угол В.
Ответы
Автор ответа:
13
Ответ:
60°
Объяснение:
Способ 1.
По теореме, обратной теореме Пифагора, проверим, не является ли треугольник прямоугольным. Должно выполняться равенство:
ВС² = АС² + АВ²
6² = (3√3)² + 3²
36 = 27 + 9
36 = 36 - равенство верно.
ΔАВС прямоугольный с гипотенузой ВС = 6.
Катет АВ в два раза меньше гипотенузы, значит он лежит против угла в 30°,
∠С = 30°.
Сумма острых углов прямоугольного треугольника равна 90°, тогда
∠В = 90° - ∠С = 90° - 30° = 60°
_____________________________
Способ 2.
По теореме косинусов:
АС² = AB² + BC² - 2 · AB · BC · cos∠B
(3√3)² = 3² + 6² - 2 · 3 · 6 · cos∠B
27 = 9 + 36 - 36 · cos∠B
36 · cos∠B = 18
cos∠B = 18 / 36 = 0,5, ⇒
∠B = 60°
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: MACHOOOOO
Предмет: Химия,
автор: sioanuytacom
Предмет: ОБЖ,
автор: stllena
Предмет: Математика,
автор: minavar
Предмет: Математика,
автор: 18612