Question

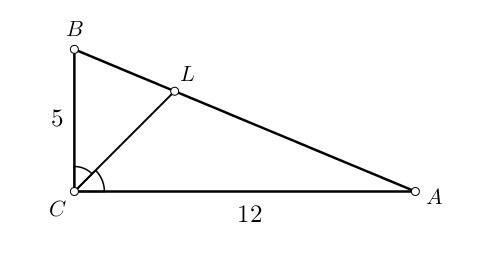
В прямоугольном треугольнике катеты равны 12 и 5 соотвественно. Найдите длины отрезков, на которые делить гипотенузу биссектриса прямого угла

Answer 1

Найдём длину гипотенузы $AB$ (см. обозначения на рисунке) по теореме Пифагора:

$|AB|^2=12^2+5^2=144+25=169\\|AB|=\sqrt{169}=13$

Длины отрезков, на которые биссектриса делит сторону, пропорциональны длинам прилежащих сторон:

$\dfrac{|BL|}{|BC|}=\dfrac{|AL|}{|AC|}$

Пусть $|BL|=x$, тогда $|AL|=13-x$:

$\dfrac{x}{5}=\dfrac{13-x}{12}\\\\12x=65-5x\\17x=65, \qquad x=\dfrac{65}{17}.$

Тогда $|AL|=13-\dfrac{65}{17}=\dfrac{156}{17}$

Ответ: 65/17 и 156/17.