Помогите решить алгебру функции | 90 баллов
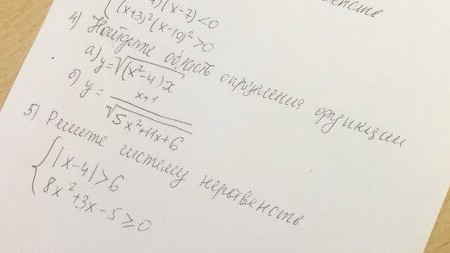
Ответы
4a) Выражение под корнем чётной степени должно быть неотрицательным, то есть ≥ 0 .
(x² - 4)x ≥ 0
x(x - 2)(x + 2) ≥ 0
- + - +
_________[- 2]__________[0]__________[2]_________
////////////////////////// ///////////////////////
x ∈ [- 2 , 0] ∪ [2 ; + ∞)
4б) Так как корень квадратный в знаменателе, то подкоренное выражение должно быть строго больше нуля.
5x² + 11x + 6 > 0
Приравняем квадратный трёхчлен к нулю и найдём его корни:
5x² + 11x + 6 = 0
D = 11² - 4 * 5 * 6 = 121 - 120 = 1
5(x + 1)(x + 1,2) > 0
(x + 1)(x + 1,2) > 0
+ - +
____________₀_____________₀__________
- 1,2 - 1
/////////////////////////// ///////////////////////
x ∈ (- ∞ ; - 1,2) ∪ (- 1 ; + ∞)
5) | x - 4 | > 6
8x² + 3x - 5 ≥ 0
8x² + 3x - 5 = 0
D = 3² - 4 * 8 * (- 5) = 9 + 160 = 169 = 13²
8(x - 0,625)(x + 1) ≥ 0
(x - 0,625)(x + 1) ≥ 0
+ - +
____________[- 1]____________[0,625]__________
/////////////////////////// /////////////////////////////
x ∈ (- ∞ ; - 1] ∪ [0,625 ; + ∞)
Окончательный ответ : x ∈ (- ∞ ; - 2) ∪ (10 ; + ∞)