Предмет: Алгебра,
автор: rrrrtttt01
Пожалуйста помогите......................
Приложения:
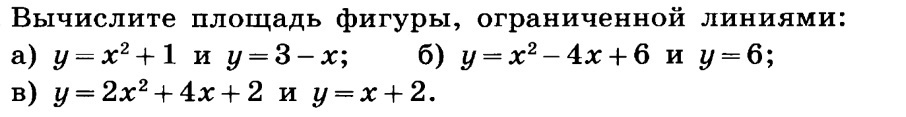
Ответы
Автор ответа:
0
а) Найдем точки пересечения графиков:
Теперь разность интегралов по найденным пределам:
Это и есть площадь.
б) Точки пересечения:
Разность интегралов:
Еще одну площадь нашли
в) Точки пересечения:
Разность интегралов:
Готово
Похожие вопросы
Предмет: Математика,
автор: tvoatanocka312
Предмет: Геометрия,
автор: santoreaydina08
Предмет: Русский язык,
автор: Flowerinikip
Предмет: Физика,
автор: ьио
Предмет: Литература,
автор: чччффф