Question

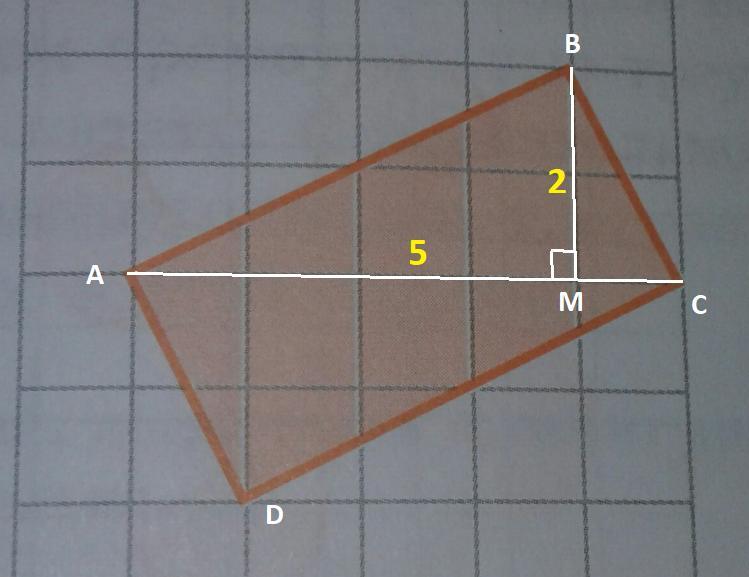
найдите площадь прямоугольника, изображенного на рисунке 19.11 (стороны квадратных клеток равны 1)

Answer 1

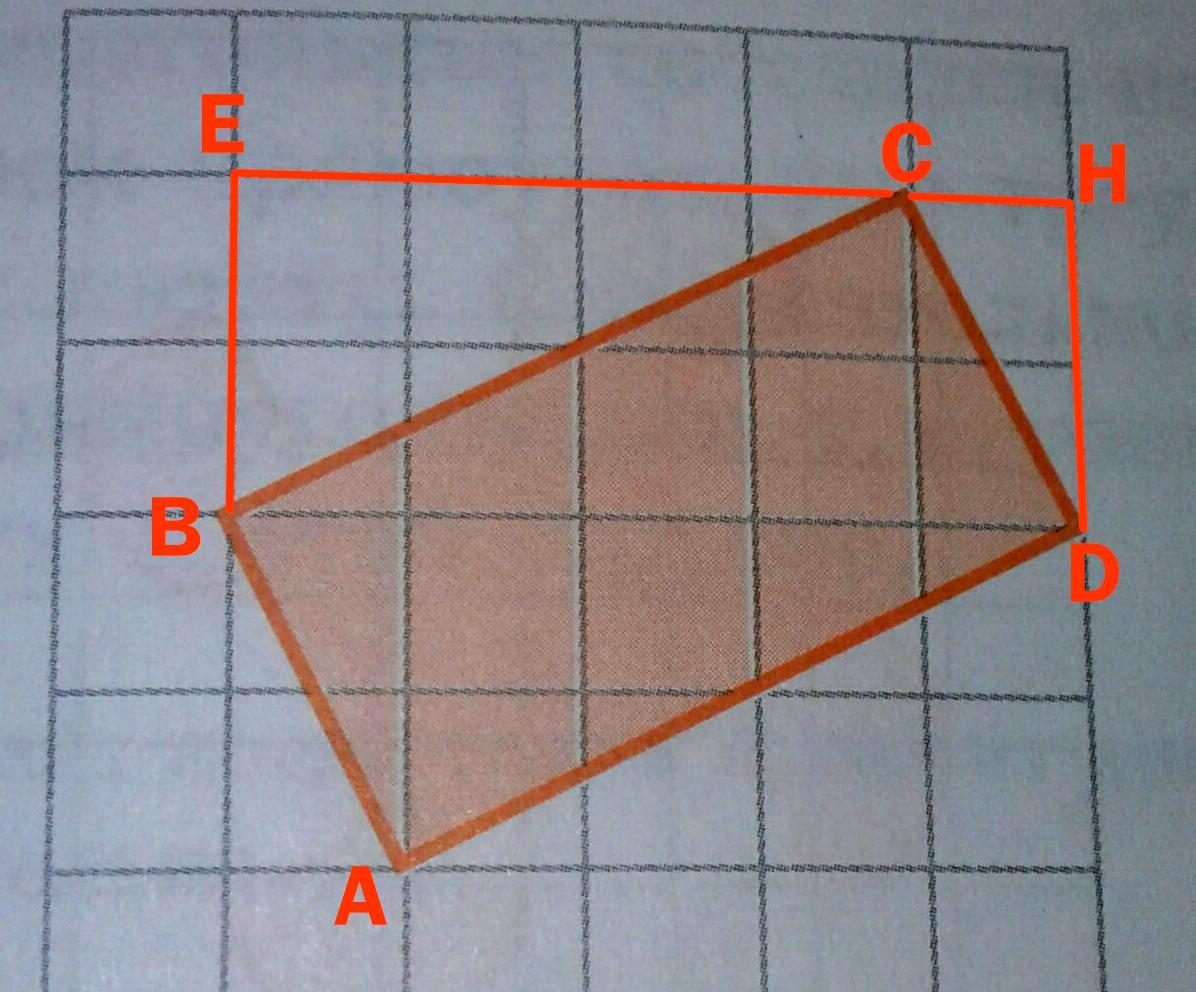
Обозначим вершины прямоугольника и проведём дополнительные отрезки как на рисунке ниже (смотрите во вложении).

Рассмотрим прямоугольный ΔВЕС.

ВЕ = 2 (ед) (так как занимает две клетки)

ЕС = 4 (ед) (так как занимает четыре клетки).

• Сумма квадратов катетов равна квадрату гипотенузы (теорема Пифагора).

Следовательно -

ВС² = ЕС² + ВЕ²

ВС² = 4² + 2²

ВС² = 16 + 4

ВС² = 20

ВС = √20 (ед).

Теперь рассмотрим прямоугольный ΔСНD.

Аналогично -

СН = 1 (ед)

HD = 2 (ед).

По теореме Пифагора -

CD² = HD² + CH²

CD² = 2² + 1²

CD² = 4 + 1

CD² = 5

CD = √5 (ед).

• Площадь прямоугольника равна произведению его смежных сторон.

То есть -

S(ABCD) = BC*CD

S(ABCD) = √20 (ед)*√5 (ед)

S(ABCD) = √100 (ед²)

S(ABCD) = 10 (ед²).

Ответ :

10 (ед²).

Answer 2

Дано : ABCD - прямоугольник,  1 кл = 1 ед.

Найти : S - ?

Решение :

Проведём диагональ АС = 5 кл = 5 ед . Диагональ прямоугольника делит его на два равных прямоугольных треугольника :  ΔABC = ΔADC.

Проведём высоту BM⊥AC, BM = 2 кл = 2 ед.

Площадь треугольника равна полупроизведению стороны на высоту, проведённую к этой стороне.

$S_{\triangle ABC}=\dfrac {AC\cdot BM}2$

Так как  ΔABC = ΔADC , следовательно, площади этих треугольников тоже равны.  Тогда площадь прямоугольника

$S_{ABCD}=S_{\triangle ABC}+S_{\triangle ADC}=2S_{\triangle ABC}=\\\\=2\cdot\dfrac{AC\cdot BM}2=AC\cdot BM=5\cdot 2=10$

Ответ : 10  ед²