Предмет: Алгебра,
автор: kotmaksim
первый пример,правилом Лопиталя
Приложения:
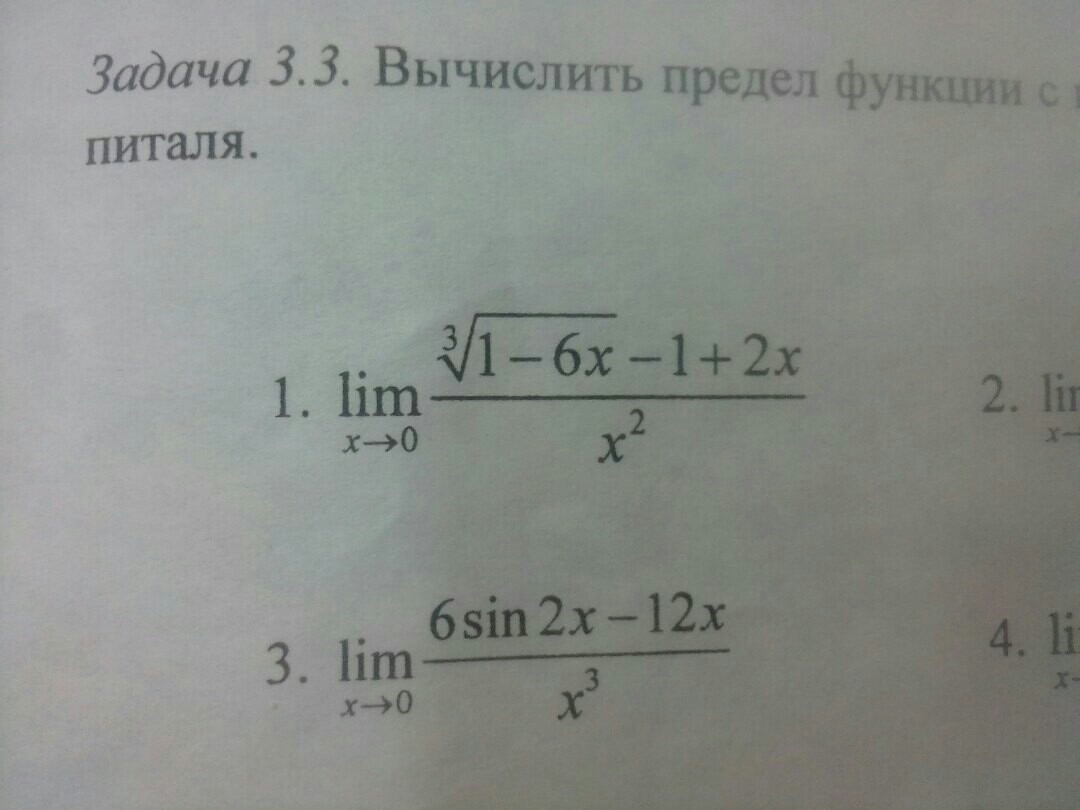
NNNLLL54:
ЛОПИТАЛЬ ...
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: Lissssskaaa
Предмет: Физика,
автор: uiluejn
Предмет: Русский язык,
автор: ruslanruslanov536
Предмет: История,
автор: Bambuk2002
Предмет: Обществознание,
автор: shirkoalla1