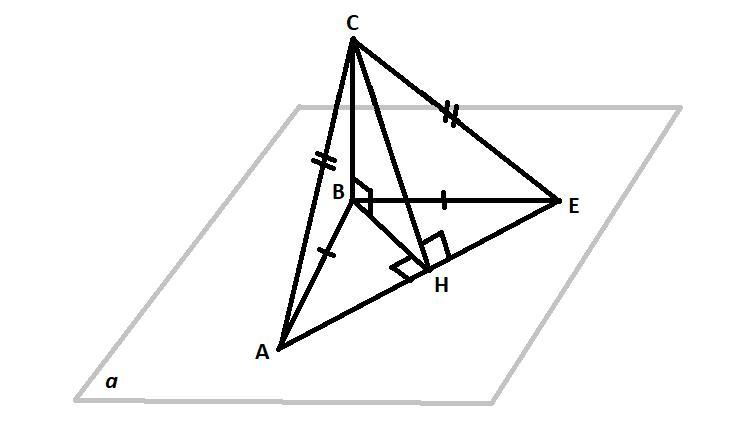
Равнобедренный треугольник ABE находится в плоскости α . Боковые стороны треугольника ABE равны по 10 см, а сторона основания AE= 16 см. К этой плоскости проведены перпендикуляр CB , который равен 4 см, и наклонные CA и CE . Вычислите расстояние от точки C до стороны треугольника AE .
Расстояние равно
−−−−−−√ см
Ответы
ΔABE - равнобедренный ⇒ Опустим из точки В на основание АЕ высоту ВН ⇒ АН = НЕ = AE/2 = 8 см.
Высота равнобедренного треугольника, проведенная к его основанию, является медианой и биссектрисой.
CB⊥α ⇒ CB⊥(ABE)
Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости.
CB⊥AB, CB⊥BE, CB⊥AE, CB⊥BH
ΔCBA = ΔCBE по двум катетам:
- СВ - общая сторона
- АВ = ВЕ - из равнобедренного ΔАВЕ
Значит, АС = СЕ ⇒ ΔАСЕ - равнобедренный.
В ΔАСЕ опустим из точки С на основание АЕ высоту. Высота должна пройти через середину АЕ, то есть через точку Н.
Следовательно, расстояние от точки C до стороны треугольника AE равно СН, ρ (С;АЕ) = СН - искомое расстояние.
В ΔАВН (∠ВНА = 90°): По теореме Пифагора
АВ² = ВН² + АН²
ВН² = АВ² - АН² = 10² - 8² = 100 - 64 = 36
ВН = 6 см
В ΔСВН (∠СВН = 90°): По теореме Пифагора
СН² = СВ² + ВН² = 4² + 6² = 16 + 36 = 52
Значит, СН = √52 = 2√13 см.
Ответ: 2√13 см