Question

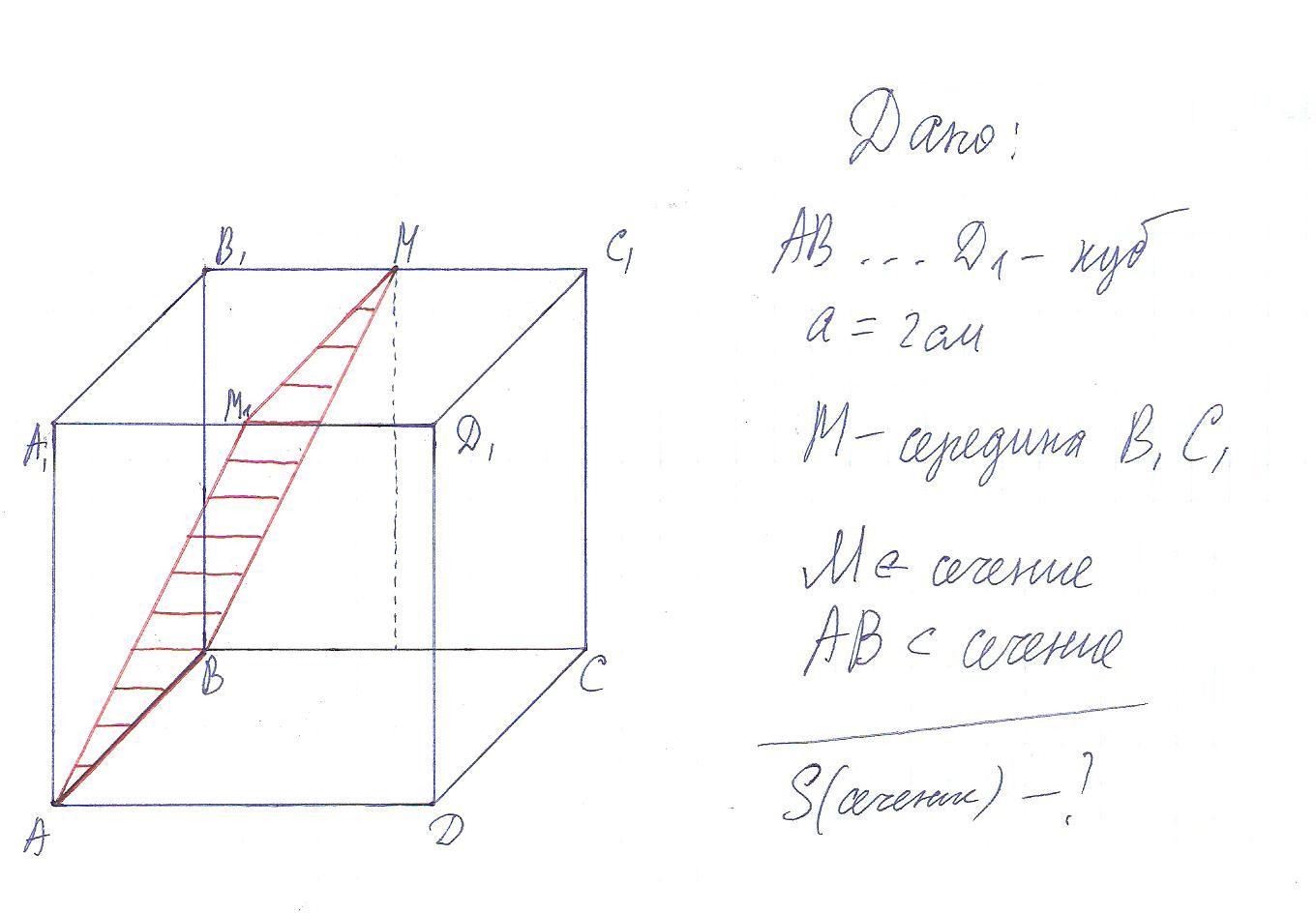
найти площадь сечения плоскостью куба проходящей через ребро АВ и середину ребра В1С1, если ребро куба равно 2 см.

Answer 1

Впишем куб в координатную плоскость x;y;z 
Тогда координата точки $A(0;0;2)\ M(1;2;0)$
Получиться треугольник АВМ, длина стороны $BM=sqrt{2^2+1^2}=sqrt{5}\ AM=sqrt{1^2+2^2+2^2}=3\ AB=2$
$M_{1}(1;2;2)\ BM_{1}=sqrt{1^2+2^2+2^2}=3\ cos(BM MM_{1})=frac{9-4-5}{-4sqrt{5}}=0\ a=90\ S=2*sqrt{5}$зная стороны найдем площадь , по теореме косинусов угол допустим между сторонами  $BM AM\ 4=5+9-6sqrt{5}cosa\ cosa=frac{sqrt{5}}{3}\ sina=frac{2}{3}\ S_{ABM}=frac{3*sqrt{5}*frac{2}{3}}{2}=sqrt{5}$

Answer 2

Сечение многогранника – многоугольник, составленный из отрезков, которые принадлежат и секущей плоскости многогранника и граням(!!!) многогранника.

Answer 3

чье решение мне списать?))

Answer 4

Построение:
Отрезки АВ и ВМ проводим, так как их концы лежат в одной плоскости. Так как сечение пересекает параллельные плоскости по параллельным прямым, то  сечение будет проходить через прямую ММ1 || AB, где М1 - середина ребра А1D1. Точки АМ1 соединяем, так как они лежат в одной плоскости.

Анализ:
В сечении получен параллелограмм АВММ1 (противоположные грани куба параллельны). Докажем, что это прямоугольник. Так как АВ и ВС - перпендикулярные прямые (ребра куба) и АВ и ВВ1 - перпендикулярные прямые (ребра куба), то прямая АВ перпендикулярная плоскости ВВ1С1С, а значит и любой прямой, лежащей в ней, в том числе и прямой ВМ. Значит угол АВМ=90 и в сечении лежит прямоугольник.

Решение:
$S_{ABMM_1}=ABcdot BM=ABcdot sqrt{BB_1^2+B_1M^2} \ S=acdot sqrt{a^2+(0.5a)^2}= frac{a^2 sqrt{5} }{2} \ S= frac{2^2 sqrt{5} }{2} =2 sqrt{5}(sm^2)$

Ответ: $2 sqrt{5}$ см^2

Answer 5

у кого-то неправильно)