Предмет: Геометрия,
автор: hdhsq
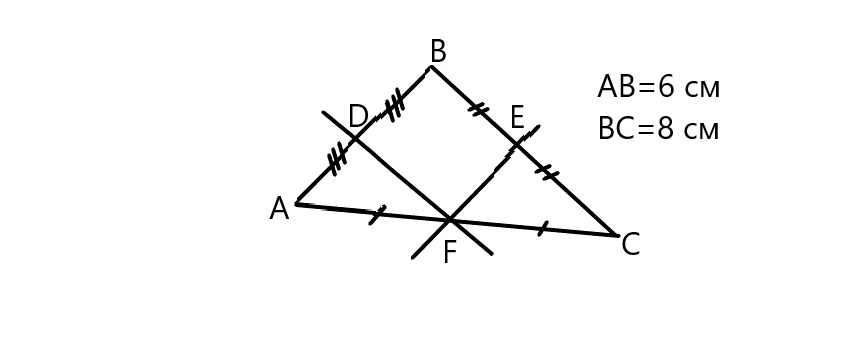
В треугольнике ABC AB=6 см, BC=8 см.Через середину стороны AC проведены прямые, параллельные сторонам AB и BC.Найдите периметр образовавшегося четырёхугольника.
Ответы
Автор ответа:
23
Свойства средней линии треугольника - параллельна стороне к которой проведена и проходит через середины смежных сторон.
Обозначим точки пересечения прямых со сторонами треугольника: D, E, F. Тогда:
FE - средняя линия треугольника АВС проведенная к стороне АВ и равна АВ/2=3 см;
DF - средняя линия треугольника АВС проведенная к стороне ВС и равна ВС/2=4 см;
DB=EF, BE=DF - средние линии проходят через середину сторон треугольника. Периметр DBEF=(3+4)*2=14 см.
Приложения:
hdhsq:
окей,тебе тоже спасибо)
Похожие вопросы
Предмет: Французский язык,
автор: dosimjankurmanbekkz
Предмет: Русский язык,
автор: demidsavenko485
Предмет: Литература,
автор: altynaisyper
Предмет: Математика,
автор: timaka4ok
Предмет: Математика,
автор: составитьдиалог