Предмет: Алгебра,
автор: xxxӃϼϒϮѺѝxxx
Помогите, пожалуйста!!!
Приложения:
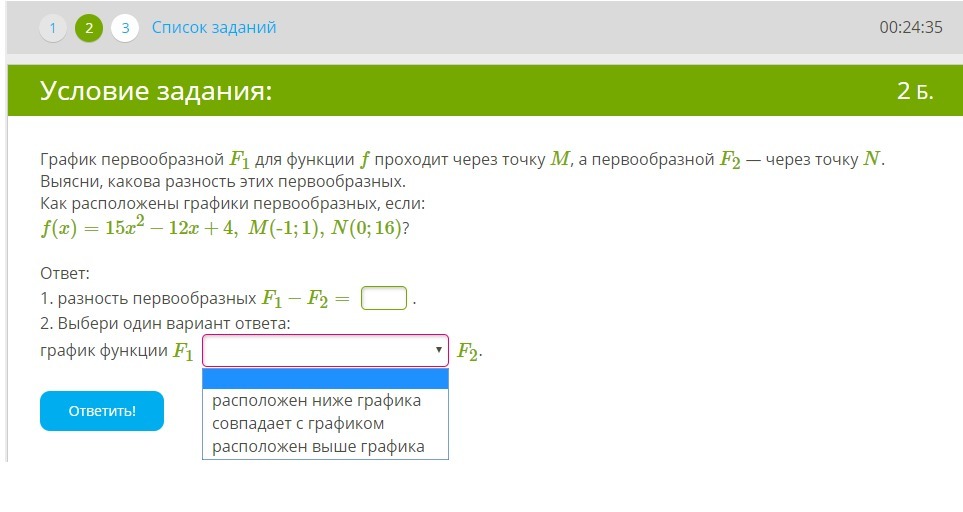
Ответы
Автор ответа:
0
<!--c-->
Так как, f(x)=6x2−12x+6,то общая первообразная F(x)=2x3−6x2+6x+C.
Вычислим C для каждой из заданных первообразных:
f(x)=6x2−12x+6,M(−1;1),N(0;6)
1.
F1(−1)=12⋅(−1)3−6⋅(−1)2+6⋅(−1)+C1=1C1=15
Итак, первая первообразная F1(x)=2x3−6x2+6x+15
2.
F2(0)=62⋅03−6⋅02+6⋅0+C2=6C2=6
F2(x)=2x3−6x2+6x+6
3. Вычислим разность этих первообразных:
F1(x)−F2(x)=(2x3−6x2+6x+15)−(2x3−6x2+6x+6)=15−6=9
Так как 9>0, то график первой первообразной F1расположен выше графикаF2.
Графики первообразных схематично изображены на рисунке:
Приложения:
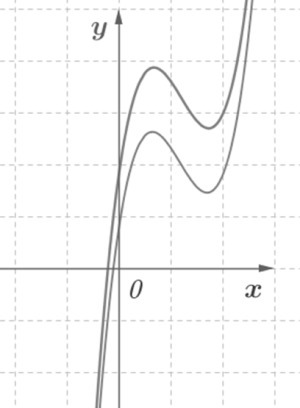
NNNLLL54:
точка дана N(0;16)
сорян, не заметила
так исправьте
Автор ответа:
0
Графики F₁(х) и F₂(х) совпадают.
Приложения:
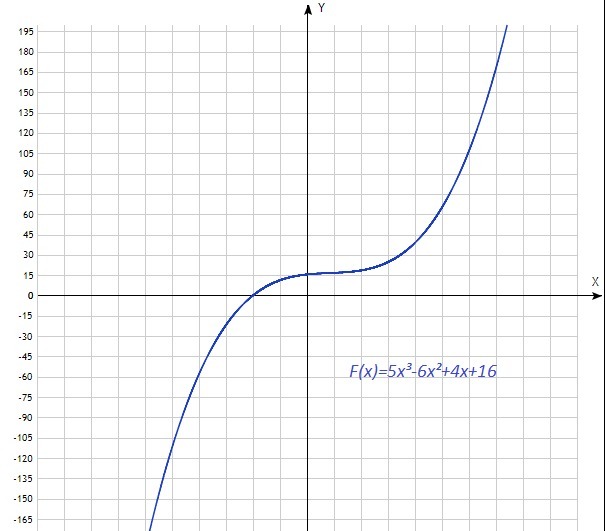
Похожие вопросы
Предмет: Химия,
автор: vikki9655
Предмет: Математика,
автор: CAXAPOK282
Предмет: Математика,
автор: l85385063
Предмет: История,
автор: Кому1надо1тот1поймет
Предмет: Математика,
автор: Millinika