Question

изобразите сечение единичного куба A... D1, проходящее через середины рёбер AD, B1C1 и точку на ребре BC, отстоящую от вершины B на 0,25. Найдите его площадь, пожалуйста помогите

Answer 1

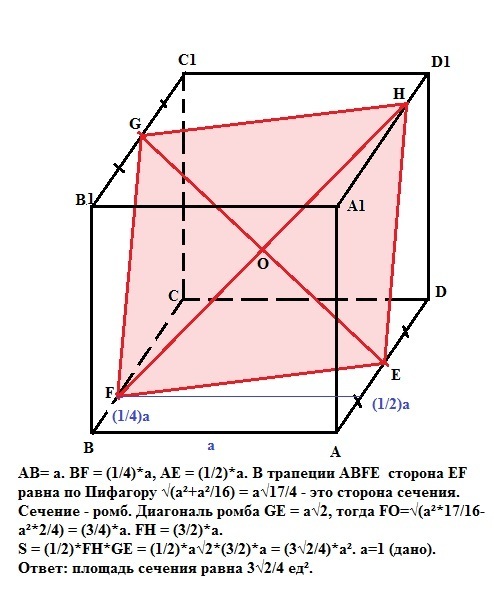
Пусть сторона куба равна a. BF = (1/4)*a, AE = (1/2)*a. Это дано. В трапеции АВFE  сторона EF равна по Пифагору √(a²+a²/16) = а√17/4 - это сторона сечения. Сечение - ромб. Диагональ ромба GE = a√2 (равна диагонали грани куба, так как параллельна ей), тогда GO = a√2/2. По Пифагору FO=√(a²*17/16 - a²*2/4) = (3/4)*a.  FH = (3/2)*a.

Sefgh = (1/2)*GE*FH = (1/2)*a√2*(3/2)*a = (3√2/4)*a². а=1 (дано).

Ответ: площадь сечения равна 3√2/4 ед².