Question

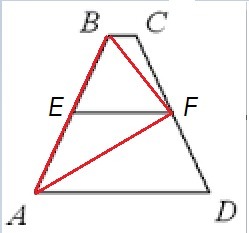
Вычислите периметр равнобокой трапеции, в которой средняя линия равна 1 и из середины боковой стороны другая её боковая сторона видна под прямым углом

Answer 1

Решение:

Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. EF = (BC+AD) /2 = EF = 1 ; BC+AD = 2;

<AFB - прямой угол. Треугольник AFB прямоугольный. АВ - гипотенуза.

AE=EB. EF - медиана в треугольнике AFB.  

Медиана, проведенная из вершины прямого угла, равна половине гипотенузы. AB = 2*EF = 2*1 = 2

Трапеция равнобокая. СD = AB = 2.

Периметр равен p= AB+BC+CD+AD = (AB+CD) +(BC+AD) = (2+2) + 2 = 6

Ответ: p = 6