Предмет: Алгебра,
автор: rtyuioplkjhgf
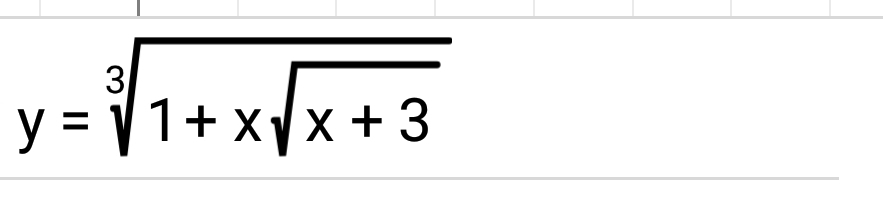
Срочно найдите производнкю функции
Приложения:
Ответы
Автор ответа:
0
y'=(³√(1+x√(x+3))'=1/3 *(1+x√(x+3))^(1/3-1)
*(√(x+3)+x*(√(x+3))'=
1/(3*(1+x√(x+3))^(2/3) *(√(x+3)+x *1/(2√(x+3))=
1/(3(1+x√(x+3))^(2/3) *
(2x+3)/(2√(x+3)
*(√(x+3)+x*(√(x+3))'=
1/(3*(1+x√(x+3))^(2/3) *(√(x+3)+x *1/(2√(x+3))=
1/(3(1+x√(x+3))^(2/3) *
(2x+3)/(2√(x+3)
армения20171:
(2х+3)/2(√(х+3)) надо (3х+6)/(2√(х+3)
Автор ответа:
0
последний ( х+1) надо (х+2)
да
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: fgjjddjkhcvnjgxcbn
Предмет: Русский язык,
автор: diezzzo4ka84
Предмет: Математика,
автор: анна0908
Предмет: Математика,
автор: karina5011